Homework 5

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

  1. Draw a coordinate plane and graph the points $(1,2), (2, -1), (-3, -4)$ and $(4, -3)$.
  2. Sketch a graph of the following equations by picking points:
    1. $x - y = 1$
    2. $y = \sqrt{x}$
      Hint Pick perfect squares for $x$, i.e. $1, 4, 9, \dots$
    3. $y - x = -2$
    4. $x^2 - y = 1$
    5. $-\lvert x \rvert - 1 + y = 0$
  3. Find the $x-$ and $y-$ intercepts of the following equations.
    1. $y = x + 6$
    2. $y = x^2 - 4$
    3. $y = -\sqrt{16 - x^2}$
  4. Draw two lines in the coordinate plane; one with negative slope and one with positive slope.
  5. Find the equation of a line that passes through $(4, 4)$ and $(0, 2)$. Write your answer in slope-intercept form.
  6. Find the equation of a line that passes through $(-2, 5)$ and $(0, 2)$. Write your answer in slope-intercept form.
  7. Find the equation of a line with slope $-3$ and passes through the point $(1,1)$. Write your answer in slope-intercept form.
  8. Find the equation of a vertical line that passes through $(-2, 4)$.
  9. Find the equation of a horizontal line that passes through $(-3, -3)$.
  10. Suppose I have an expression $f(x)$ and I find two different inputs that give the same evaluation. In particular, I find that $x = 2$ and $x = 3$ gives $f(2) = f(3)$. Is $f$ a function?
  11. Suppose I have an expression $f(x)$ and I find one input which gives two different evaluations. In particular, I find that $x = 2$ spits out $f(2) = 5$ and $f(2) = 3$. Is $f$ a function?
  12. Write down two examples of functions in your daily life.
  13. Suppose your friend was given a function \[f(x) = x^2 - 3\] and they are asked to find $f(x + h) - f(x)$. Your friend ends up writing \[f(x + h) - f(x) = x^2 - 3 + h - x^2 - 3\] Identify the two mistakes that were made.
  14. Let $f(x) = x^2 - x + 1$. Evaluate and simplify the following:
    1. $f(1)$
    2. $f(a)$
    3. $f(-a)$
    4. $f(x + h)$
    5. $\dfrac{f(x + h) - f(x)}{h}$
  15. Let $f(x) = \dfrac{1}{x}$. Evaluate and simplify the following:
    1. $f(-1)$
    2. $f(x + h)$
    3. $\dfrac{f(x + h) - f(x)}{h}$
  16. Let $f(x) = 2x^2 - x$. Evaluate and simplify the following:
    1. $f(0)$
    2. $f(x + h)$
    3. $\dfrac{f(x + h) - f(x)}{h}$
  17. Suppose $f$ is a function. What two types of numbers do you need to remove when finding the domain?
  18. Find the domain of the following functions:
    1. $f(x) = \dfrac{1}{x - 1}$
    2. $f(x) = \dfrac{1}{x^2 + 3x + 2}$
    3. $f(x) = \dfrac{x^2 - 2x + 1}{x - 1}$
    4. $f(x) = \dfrac{x^2}{(x^2-1)(x^2-4)}$
    5. $f(x) = \sqrt{2x - 1}$
  19. Find the domain of the following functions:
    1. $f(x) = \dfrac{1}{\sqrt{2x - 1}}$
    2. $f(x) = \dfrac{1}{x\sqrt{2x - 4}}$
      Hint Use the zero product property when setting denominator to zero.
    3. $g(x) = \sqrt{x-2} - \dfrac{2x}{\sqrt{-x + 3}}$
  20. Let \[f(x) = \begin{cases} 3x + 2 & x \geq 2 \\ x^2 - x & x < 2\end{cases}\] Evaluate the following:
    1. $f(0)$
    2. $f(1)$
    3. $f(2)$
    4. $f(3)$
    5. $f(4)$
  21. Let \[f(x) = \begin{cases}-1 & x < -1 \\ x & -1 \leq x \leq 1 \\ -1 & x > 1\end{cases}\] Evaluate the following:
    1. $f(-2)$
    2. $f(-1)$
    3. $f(0)$
    4. $f(0.99)$
    5. $f(1)$
    6. $f(2)$
  22. Sketch a graph on the coordinate plane for the following functions using the table. Feel free to verify your graphs with Desmos.
    1. $f(x) = 1-x^2$
    2. $g(x) = x^3 + 1$
    3. $f(x) = \begin{cases} -x - 1 & x \leq 1 \\ x + 1 & x > 1\end{cases}$
    4. $f(x) = \begin{cases} x & x > 1 \\ x^2 - 1 & x \leq -1\end{cases}$
    5. $f(x) = \begin{cases} 1 & x \geq 2 \\ -1 & x < 2 \end{cases}$
    6. $g(x) = \begin{cases} x & x > 0 \\ 1 & x = 0 \\ -2x + 3 & x < 0 \end{cases}$
  23. Draw a curve in the plane that is not the graph of a function.
  24. Is this expression a function? Why or why not? \[f(x) = \begin{cases}x^2 - 3 & x \geq 0 \\ -x - 4 & x \leq 0\end{cases}\]
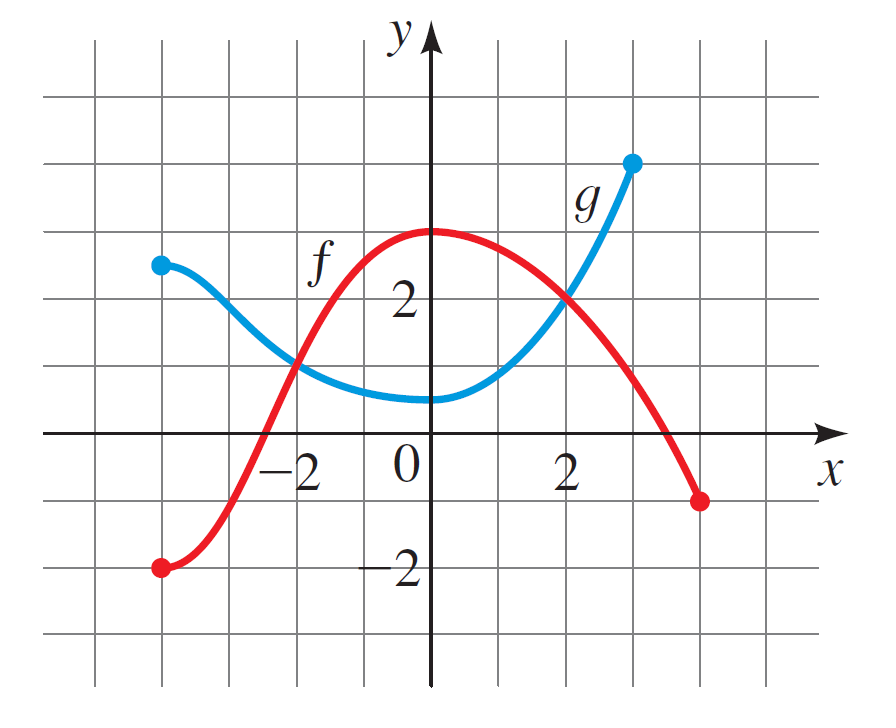
  25. Given the two functions $f$ and $g$
    1. What is $f(0)$?
    2. What is $g(3)$?