3.2: Polynomial Functions and Their Graphs

What Are We Doing?

This section wil show you:

what graphs of polynomials look like.
how to graph a polynomial by hand using end behavior and $x$-intercepts.

Vocabulary

Here's the definition of a polynomial with some extra identifiers:

polynomial function
A polynomial function of degree $n$ is a function of the form \[P(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0 \qquad a_n \neq 0\] where $n$ is an integer.

$a_n, a_{n-1}, \dots, a_1, a_0$ are called the coefficients.
$a_0$ is called the constant coefficient or constant term.
$a_n$ is called the leading coefficient.
$a_nx^n$ is called the leading term.

Suppose \[-3x^5 + 6x^4 - 2x^3 + x^2 + 7x + 6\] Identify the degree, leading term, leading coefficient, and constant coefficient.

Monomials

A monomial has the form $P(x) = x^n$. These graphs have three possible types of shapes, depending on $n$:

$n = 1$ $n$ is even $n$ is odd

$n = 1$

$n$ is even

$n$ is odd

Sketch an accurate graph of $f(x) = (x-2)^4$.

The monomial shapes are important to remember. Their shapes, as we will see, appear in the graph of every polynomial.

Polynomial Graphs

Polynomials have domain $\mathbb{R}$, and their graphs are continuous:

Informal Definition: continuity
A graph is continuous if you can draw it without lifting your pencil.

In Calculus, you will learn the official definition.

Moreover, there cannot be any corners or sharp corners (cusps):

Not Graphs of Polynomials Graphs of Polynomials

Not Graphs of Polynomials

Graphs of Polynomials

Polynomial graphs can be broken up into two main ideas: end behavior and zeros.

End Behavior

Let's start with the "ends" of the graph. First, notation:

$y\rightarrow \infty$ means $y$ grows without bound. Meaning, $y$ is bigger than any number you can think of!
$y\rightarrow -\infty$ means $y$ decreases without bound.

end behavior

The end behavior of a polynomial depends on the degree $n$ and the leading coefficient $a_n$:

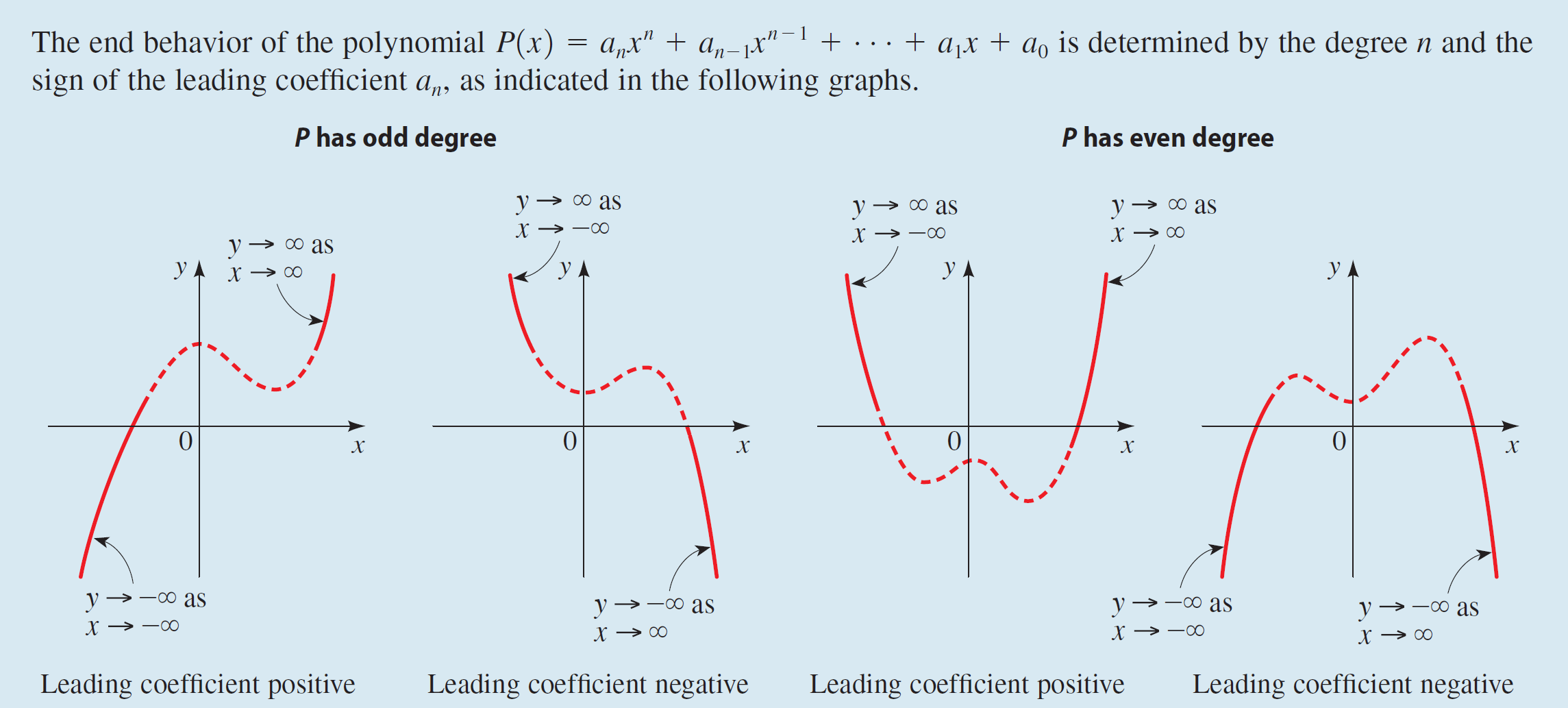
Determine the end behavior of $P(x) = -2x^4 + 5x^3 + 4x - 7$.

Determine the end behavior of $P(x) = -(2x-2)^2(x-4)^3$.

Zeros ($x$-intercepts)

Now we look between the "ends".

zeros
Suppose $P$ is a polynomial and $c$ is a real number. Then the following are equivalent:

$c$ is a zero of $P$.
$c$ is a $x$-intercept of the graph of $P$.
$x = c$ is a solution of the equation $P(x) = 0$. Meaning, $P(c) = 0$.
$(x - c)$ is a factor of $P(x)$.

Find the zeros of $P(x) = x^2 + x - 6$.

Intermediate Value Theorem for Polynomials
If $P$ is a polynomial and $P(a)$ and $P(b)$ have opposite signs, then there exists at least one value $c$ between $a$ and $b$ where $P(c) = 0$.

Consequence of IVT: between two successive zeros, $P(x) > 0$ or $P(x) < 0$.

Putting it all together:

Graphing Polynomials

Find zeroes: Factor and solve for $x$.
IVT test points: Make a sign diagram of $P(x)$ and whether it's $+$ or $-$ between two successive zeros.
Find end behavior.
Graph: Connect the end behavior, signs, and zeros in a smooth and continuous fashion.

Sketch a graph of $P(x) = (x+2)(x-1)(x-3)$.

Sketch a graph of $P(x) = x^3 - 2x^2 - 4x + 8$.

In this example, $(x-2)^2$ looks like a parabola near $x = 2$ (think horizontal shift from $x^2$ right two units).

The power tells you the shape. They correspond to the monomial shapes.

Shape of a Graph Near a Zero

zero of multiplicity $m$
$c$ is a zero of multiplicity $m$ if $(x - c)^m$ appears in the factorization of $P$.

Graph Shape Near Zeros of Multiplicity $m$
If $c$ is a zero of multiplicity $m$, then the graph shape near $c$ corresponds is as follows:

$n$ odd, $n \neq 1$

$n$ even

$n$ odd,
$n \neq 1$

$n$ even

Graph the polynomial $P(x) = x^2(x-2)^3(2x+1)^2$.