Homework 2
Directions:
- Show each step of your work and fully simplify each expression.
- Turn in your answers in class on a physical piece of paper.
- Staple multiple sheets together.
- Feel free to use Desmos for graphing.
Answer the following:
- Is the point $P\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$ on the unit circle? Show using calculations.
- What is the reference number $\bar{t}$? What is the range of values $\bar{t}$ is allowed to be?
- Find the following terminal points $P$ associated with the following $t$ values:
- $t = 0$
- $t = \frac{3\pi}{2}$
- $t = \frac{2\pi}{3}$
- $t = \frac{5\pi}{6}$
- $t = -\frac{2\pi}{3}$
- $t = -\frac{9\pi}{4}$
- $t = -\frac{11\pi}{6}$
- $t = 1000\pi + \frac{2\pi}{3}$
- $t = -83\pi + \frac{\pi}{3}$
- $t = \pi + 2\pi - 3\pi + \frac{4\pi}{3}$
- $t = \dfrac{81\pi}{6}$
- Find the six trigonometric functions of $t = \dfrac{2\pi}{3}$.
- Find the six trigonometric functions of $t = -\dfrac{5\pi}{6}$.
- Find the six trigonometric functions of $t = \dfrac{43\pi}{6}$.
- Using the terminal point associated with $t = \dfrac{\pi}{2}$, explain why $\tan\left(\dfrac{\pi}{2}\right)$ does not exist.
- A function usually has the notation $y = f(x)$, meaning you plug in $x$ into $f$ and the result is called $y$.
Let $x \in \mathbb{R}$ and $P(a, b)$ be the associated terminal point. What should the value of $y$ in the equation \[y = \cos x\] be? - If $\sin t > 0$ and $\cos t < 0$, what quadrant is the terminal point in?
- If $\cos t < 0$ and $\cot t < 0$, what quadrant is the terminal point in?
-
Consider the function \[f(t) = \sin (t) \cos (t)\]
Determine if $f(t)$ is positive or negative when the terminal point $P$ associated with $t$ is in Quadrant I, II, III, and IV.
Hint: Use the definition of the trig function + their coordinate signs. - Consider the function \[f(t) = \sec^{15}(t) \cdot \left[1 - \tan(t)\right]^6\] Determine if $f(t)$ is positive or negative when the terminal point $P$ associated with $t$ is in Quadrant I, II, III, and IV.
- Suppose $t \in \mathbb{R}$.
- What is the maximum value $\sin (t)$ could be? How about the minimum value?
- Answer the two questions above for $\cos (t)$.
- Fill out this table. It will probably be helpful in the future.
$t$ $\tan(t)$ $0$ $\frac{\pi}{6}$ $\frac{\pi}{4}$ $\frac{\pi}{3}$ $\frac{\pi}{2}$ - $P\left(-\dfrac{3}{5}, -\dfrac{4}{5}\right)$ is a terminal point associated with some $t \in \mathbb{R}$. Determine the values of $\sin(t), \cos(t)$ and $\tan(t)$.
- Suppose a function $f(x)$ has period $23$. Write the mathematical formula describing this behavior.
-
What is the period of the following function?
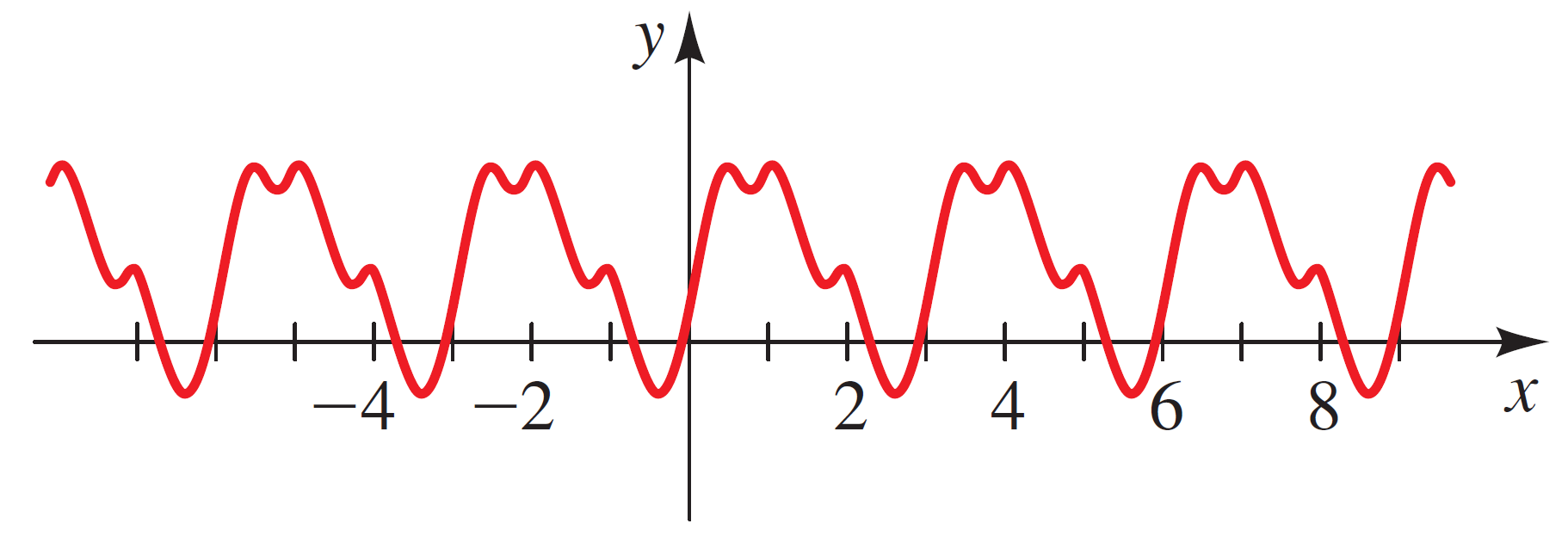
- Suppose $f(x) = \sqrt{x}$. We want to vertically shift $f(x)$ upwards 3 units and left four units to make a new function $g(x)$. What is the formula of $g(x)$?
- Starting from a base function $f(x)$, I want to create a function $g(x)$ where I apply the following transformations to $f(x)$ in the following order:
- vertically shift up three units
- horizontally shift right four units
- vertical stretch of 2 units
- horizontal shrink of $\frac{1}{3}$ units
- reflection over the $x$-axis
- Suppose \[f(x) = \sqrt{x} \qquad g(x) = \sqrt{x - 2} \qquad h(x) = \sqrt{\frac{1}{2}x - 2} \qquad i(x) = \sqrt{\frac{1}{2}\left(x-2\right)}\]
- Is $g(x)$ horizontally shifted two units to the right from $f(x)$? Why or why not?
- Is $h(x)$ horizontally shifted two units to the right from $f(x)$? Why or why not?
- Is $i(x)$ horizontally shifted two units to the right from $f(x)$? Why or why not?
- Suppose \[f(x) = x^3 \qquad g(x) = \left(\pi\left(x + 4\right)\right)^3 \qquad h(x) = \left(0.25x + 4\right)^3 \qquad i(x) =(x+4)^3\]
- Is $g(x)$ horizontally shifted four units to the left from $f(x)$? Why or why not?
- Is $h(x)$ horizontally shifted four units to the left from $f(x)$? Why or why not?
- Is $i(x)$ horizontally shifted four units to the left from $f(x)$? Why or why not?
- Graph one period of $f(x) = \cos x$ by hand.
- For each of the following functions:
1. State each relevant transformation, amplitude, and period. 2. Graph one complete period by hand. Be sure to show in the graph the endpoints of one period.
- $y = 1 + \cos (x - \pi)$
- (skip this) $f(x) = 3\cos\left(2x - \dfrac{\pi}{3}\right)$
- $g(x) = 2 - \cos\left(2\left(x - \dfrac{\pi}{3}\right)\right)$
- (skip this) $h(x) = \sin(\pi + 2x)$
- (skip this) $y = 5\sin\left(\pi x + \dfrac{\pi^2}{3}\right)$
- (skip this) $y = -5 + 4\cos(\pi - x)$
- (skip this) For each of the following functions:
1. State each relevant transformation. 2. Graph one complete period by hand. Be sure to show in the graph where one period beings and ends.
- $y = 5\sec x$
- $f(x) = 2\csc \left(\pi x - \dfrac{\pi^2}{2}\right)$
- $y = 2\cot\left(x - \dfrac{\pi}{3}\right)$
- $y = 1 + \tan\left(\pi x\right)$
- $y = 4 \tan (3x - 2\pi)$