Homework 5
Directions:
- Show each step of your work and fully simplify each expression.
- Turn in your answers in class on a physical piece of paper.
- Staple multiple sheets together.
- Feel free to use Desmos for graphing.
Answer the following:
- You are driving a car with 24 inch diameter wheels. On Foothill Blvd, your linear speed is 40 miles/hour. Find the angular speed (in rad/hour) and the number of revolutions completed per hour.
- Planet Earth is about 93,000,000 miles from the sun and can be modelled with circular motion around the Sun.
- If the Earth completes one revolution per year, calculate the angular speed (in rad/hour) and linear speed (in miles/hour).
- The average linear speed is 66,616 miles/hour, calculated with more advanced models because Earth is not quite in exact circular motion around the Sun. Even so, do you thinks your answer in part (a) is close to the actual average speed?
- You have probably seen this visualization of the Solar System:
This visualization, while pretty, is misleading compared to our actual reality. The Sun (therefore the Solar System) isn't just floating in space at one point. Our entire Solar System is actually moving through space!
Question: Watch this video and write a few sentences reflecting on how you feel/what you learned. Does this information change your perspective on your reality?
- You are driving a car with 29 inch diameter wheels. On the freeway, your tires complete 15 revolutions per second. Find the angular speed (in rad/sec) and linear speed rounded (in miles/hour, rounded to the nearest tenth).
- Evaluate the following:
- $\sin(120^\circ)$
- $\tan(-150^\circ)$
- $\cos(-135^\circ)$
- Suppose a right triangle $ABC$ has an acute angle $\theta$. The opposite side has length 3, adjacent length 4. Find $\sin(\theta)$.
- Sketch a triangle and it's acute angle $\theta$ that has $\tan(\theta) = \frac{10}{8}$. Label all three sides.
- A right triangle ABC has one acute angle $45^\circ$. The hypotenuse has length $16\sqrt{2}$. Solve the triangle.
- Suppose a truck has 40 inch radius wheels and a line is drawn from the center of the wheel to the right edge of the wheel. Let the current position of this line be the initial side. Assuming no acceleration, the wheel rotates at $\frac{1}{16}$ rotations per second. The truck starts moving and stops after 4 seconds. Consider the final position of this drawn line the terminal side. What is the area of the sector between the terminal and initial side?
- Why does $t = \dfrac{\pi}{3}$ give the terminal point $P\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)$?
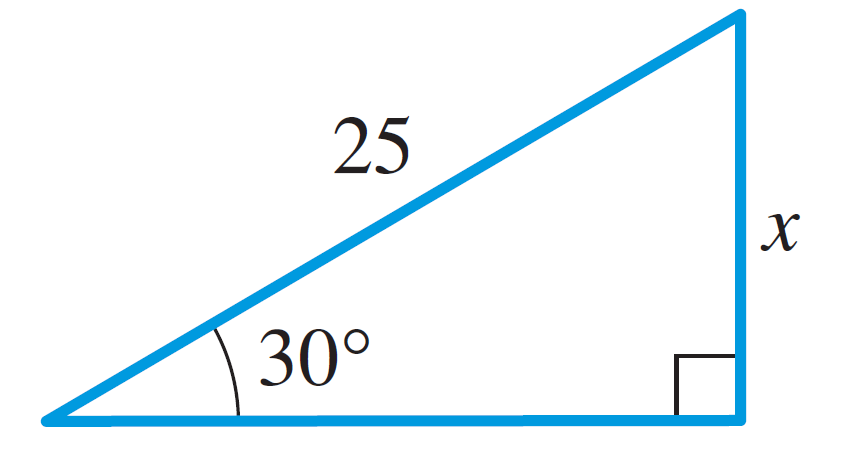
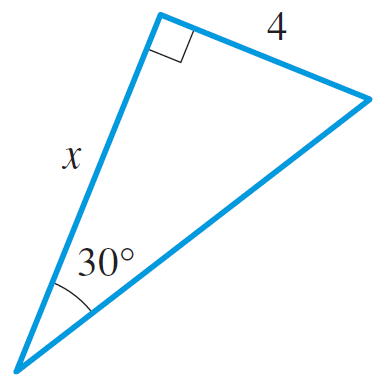
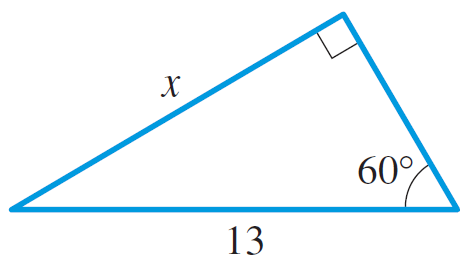
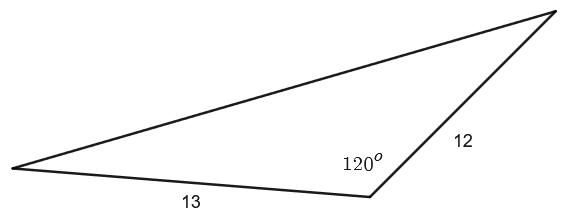
- Find the side labeled $x$:
-
- A 600-ft guy wire is attached to the top of a communications tower. If the wire makes an angle of $65^\circ$ with the ground, how tall is the communications tower?
- From the top of a 200 feet lighthouse, the angle of depression to a ship in the ocean is $23^\circ$. How far is the ship from the base of the lighthouse?
- A sequoia tree casts a shadow 100 feet long. Find the height of the tree if the angle of elevation of the sun is $45^\circ$.
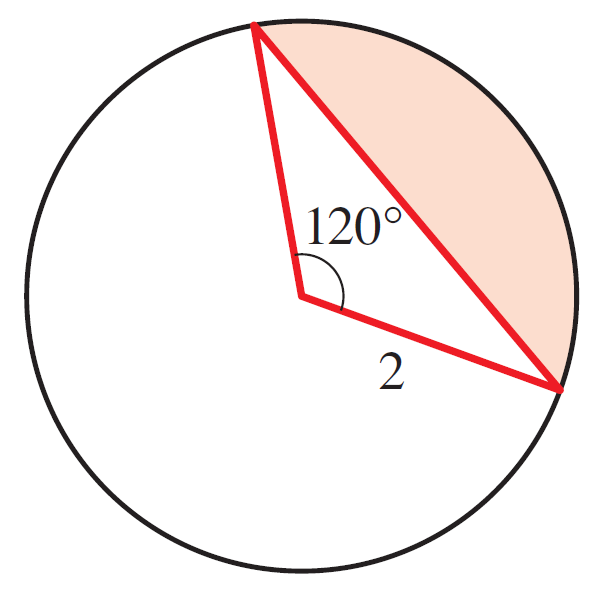
- Find the area of the shaded region.
- (skip this) Find the area of this triangle.
- Which of the following are identities? If they are not, show with specific variable values. If you think they are, justify using reasoning based off of previous sections or prove it.
- $x^2 + y^2 = 1$
- $x(y + z) = xy + xz$
- $x^2 - \cos^2 x = (x - \cos x)(x + \cos x)$
- $\sin(x + y) = \sin(x) + \sin(y)$
- Simplify these expressions:
- $\cos t \tan t$
- $\dfrac{\sec x}{\csc x}$
- $\dfrac{\sec \theta - \cos \theta}{\sin \theta}$
- $\dfrac{1}{1 + \sin \theta} + \dfrac{1}{1 - \sin \theta}$
- $\dfrac{\csc x - \cot x}{\sec x - 1}$
- $\dfrac{\cos^2 t + \tan^2 t - 1}{\sin^2 t}$
- Prove these identities algebraically:
- $\dfrac{\sin \theta}{\tan \theta} = \cos \theta$
- $\dfrac{\cos x}{\sec x\sin x} = \csc x - \sin x$
- $\dfrac{\sin \alpha \sec \alpha}{\tan \alpha} = 1$
- $\dfrac{(\sin x + \cos x)^2}{\sin x \cos x} = 2 + \sec x \csc x$
- $\sin^4 \alpha - \cos^4 \alpha = \sin^2 \alpha - \cos^2 \alpha$.
Hint: Let $x = \sin^2 \alpha, y = \cos^2 \alpha$ and factor. - $\dfrac{\cos x}{\sec x} + \dfrac{\sin x}{\csc x} = 1$
- $\tan \theta + \cot \theta = \sec \theta \csc \theta$
- $(\cot \theta - \csc \theta)(\cos \theta + 1) = -\sin\theta$
- $\dfrac{\sin \theta}{\tan \theta} = \cos \theta$
- Assume $0 < \theta < \pi/2$. Make the indicated trigonometric substitution and simplify.
- $\dfrac{x}{\sqrt{1 - x^2}}, \ x = \sin \theta$.
- $\sqrt{9 - x^2}, \ x = 3\sin \theta$
For the following three two problems, you may leave the trig function with the degrees plugged in. You do not need to evaluate the expression.
The rest of these problems will appear on next week's homework. Skip the rest of these for this homework.