6.2: Trigonometry of Right Triangles
Previously, we saw $\sin(t)$ extracted the $y$-coordinate from the terminal point, $\cos(t)$ the $x$-coordinate, and so on. Let's see how we can do the same with a right triangle.
Consider the following right triangle:
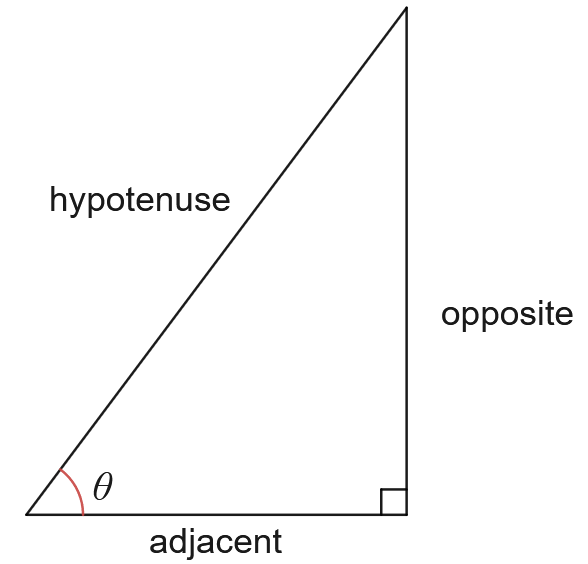Then we have
Then we have
| $\sin \theta = \dfrac{\text{opposite}}{\text{hypotenuse}}$ | $\cos \theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}$ | $\tan \theta = \dfrac{\text{opposite}}{\text{adjacent}}$ |
| $\csc \theta = \dfrac{\text{hypotenuse}}{\text{opposite}}$ | $\sec \theta = \dfrac{\text{hypotenuse}}{\text{adjacent}}$ | $\cot \theta = \dfrac{\text{adjacent}}{\text{opposite}}$ |
An acronym to remember this is SOH CAH TOA. For example, SOH means Sine Opposite Adjacent.
What's the connection between this right triangle $\sin$ definition and the definition based on the terminal point?
Suppose a right triangle has an acute angle. The opposite side is 2, adjacent is $\sqrt{5}$, and hypotense is $3$. Find $\sin \theta, \cos \theta$ and $\tan \theta$.
Suppose a right triangle has an acute angle. The opposite side is $\sqrt{7}$, adjacent is $3$, and hypotense is $4$. Find $\sin \theta, \cos \theta$ and $\tan \theta$.
Special Triangles
It's time to answer how we know the arbitrary terminal point values for $\frac{\pi}{3}$ and $\frac{\pi}{6}$. This part will be done in class.
Applications of Trigonometry of Right Triangles
A triangle is comprised of three sides and three angles. Solving a right triangle means to find the values of the three sides and three angles.
Triangle $ABC$ has $\angle A = 30^\circ, \angle C = 90^\circ$ and hypotenuse $12$. Solve $ABC$.