Homework 2

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

  1. Read (or watch the recorded lecture) these two lecture notes on trigonometric functions: 5.1: Unit Circle and 5.2: Trigonometric Functions. This is mandatory reading if you do not remember trigonometric functions.
    Draw a checkmark to get credit for this problem.
  2. Using the unit circle, explain why $\tan\left(\dfrac{\pi}{2}\right)$ is undefined.
  3. Find the six trigonometric functions of $t = \dfrac{2\pi}{3}$.
  4. Find the six trigonometric functions of $t = -\dfrac{5\pi}{6}$.
  5. Suppose \[f(x) = \sin(x) + \cos(x) \qquad g(x) = \tan(x)\] Evaluate and simplify the following expressions without a calculator/the internet:
    1. $f(0)$
    2. $g(0)$
    3. $f\left(\frac{\pi}{2}\right) + g(\pi)$
    4. $f\left(-\dfrac{46\pi}{4}\right)\cdot g\left(\dfrac{3\pi}{2}\right)$
    5. $f(0) - g(0)$
  6. You are given a function $F(x)$. Decompose $F(x)$ into two functions $f, g$ where $F = f \circ g$.
    1. $F(x) = \sin(\cos x)$
    2. $F(x) = \sin^2(x)$
    3. $F(x) = \sin(x^2)$
    4. $F(x) = (x^3 - x^2 - 1)^{2/3}$
    5. $F(x) = (x^2 - x)^2$
    6. $F(x) = \sqrt[5]{(x + 1)^3}$
    7. $F(x) = \sec(\tan(x))$
  7. Find the domain of the following functions:
    1. $f(x) = \dfrac{1}{x^2 - 1}$
    2. $f(x) = \sqrt{x} + \dfrac{1}{x}$
    3. $f(x) = \sin(x)$
    4. $f(x) = \dfrac{1}{\sqrt{x}}$
      Hint: Both problems are present.
  8. Suppose \[f(x) = \sin(x) \qquad g(x) = x^2 - x \qquad h(x) = f(x)g(x)\] Evaluate the following:
    1. $f\circ g$
    2. $g \circ f$
    3. $h \circ f$
  9. Suppose $f(x)$ is a function. Explain in English the geometric intuition behind the symbols \[\lim_{x\rightarrow a}f(x) = L\] means.
  10. Suppose \[\lim_{x\rightarrow a}f(x) = L\] Does the limit see what happens exactly at the $x$-value $a$?
  11. Suppose we have an expression $\dfrac{1}{x}$ where $x$ gets closer and closer to 0 from the right. What does the expression $\dfrac{1}{x}$ end up approaching?
  12. A function $f(x)$ has the following graph: Find the following. If they do not exist explain why.
    1. $\displaystyle\lim_{x\rightarrow 2^-} f(x)$
    2. $\displaystyle\lim_{x\rightarrow 2^+} f(x)$
    3. $\displaystyle\lim_{x\rightarrow 2} f(x)$
    4. $f(2)$
    5. $\displaystyle\lim_{x\rightarrow 4} f(x)$
    6. $f(4)$
  13. Sketch one graph of a function $f(x)$ which satisfies the following:
    1. $f(0) = -1$
    2. $f(3) = 1$
    3. $\displaystyle\lim_{x\rightarrow 0} f(x) = 1$
    4. $\displaystyle\lim_{x\rightarrow 3^-} f(x) = -2$
    5. $\displaystyle\lim_{x\rightarrow 3^+} f(x) = 2$
  14. A function $g(x)$ has the following graph: 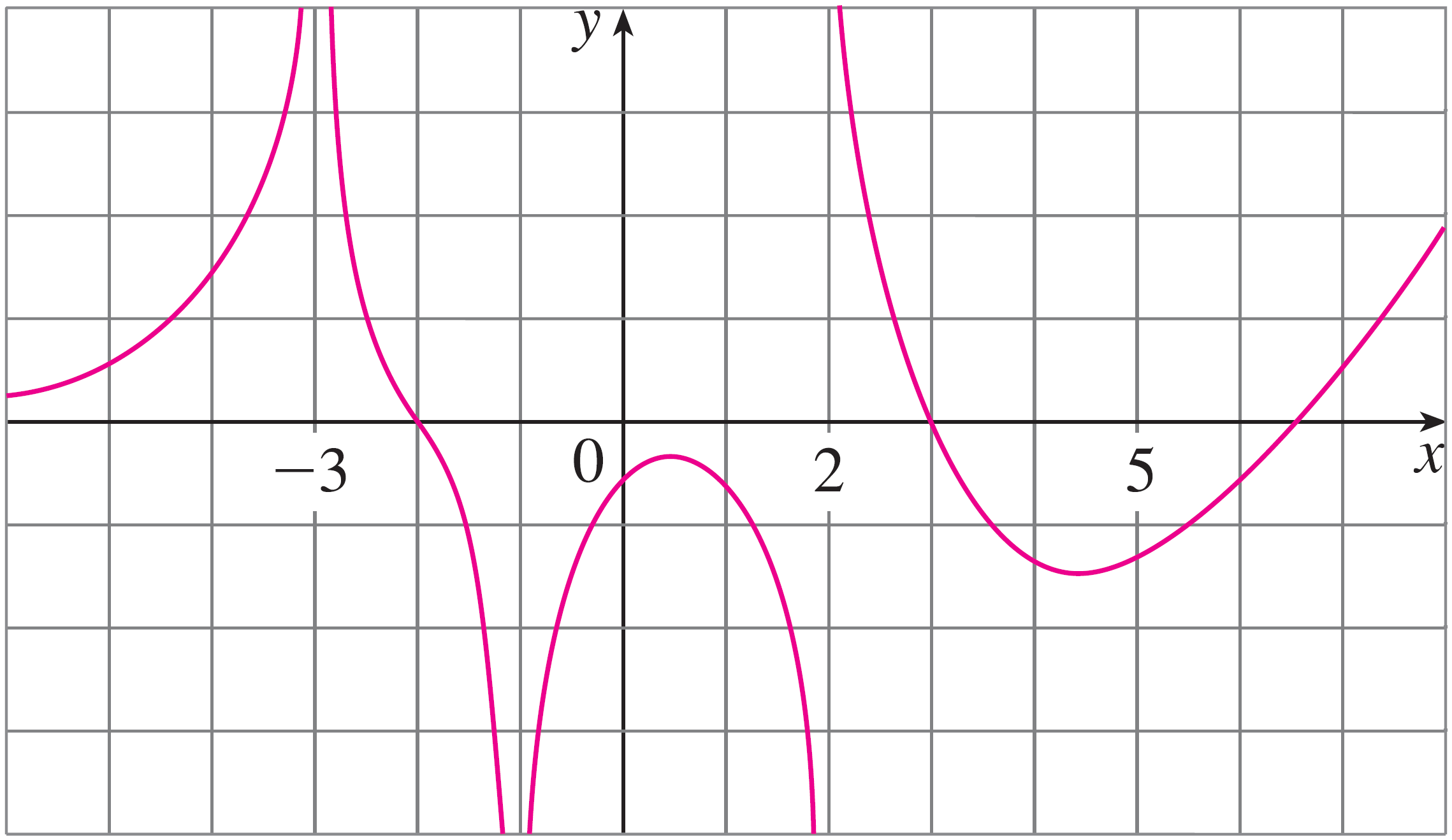Find the following. If they do not exist explain why.
    1. $\displaystyle\lim_{x\rightarrow -3} g(x)$
    2. $\displaystyle\lim_{x\rightarrow 2^-} g(x)$
    3. $\displaystyle\lim_{x\rightarrow 2^+} g(x)$
    4. $\displaystyle\lim_{x\rightarrow 2} g(x)$
    5. $\displaystyle\lim_{x\rightarrow -1} g(x)$
    6. $g(3)$
  15. Given the following functions $f(x)$ and $g(x)$: Find the following limits, if it exists. If it doesn't, explain why.
    1. $\displaystyle \lim_{x\rightarrow 2}\ [f(x) + g(x)]$
    2. $\displaystyle \lim_{x\rightarrow 1}\ [f(x) + g(x)]$
    3. $\displaystyle \lim_{x\rightarrow 0}\ [f(x)g(x)]$
    4. $\displaystyle \lim_{x\rightarrow 2}\ [x^3f(x)]$
    5. $\displaystyle \lim_{x\rightarrow 1}\ \sqrt{3 + f(x)}$
  16. Suppose $f(x)$ and $g(x)$ are two different functions. You compute the limit: \[\lim_{x\rightarrow 5} \dfrac{f(x)}{g(x)} = \cdots = \dfrac{0}{0}\]
    1. What type of result is this called?
    2. Suppose you decide to leave your answer as $\dfrac{0}{0}$. Is your answer correct and complete?
    3. What global factor do you need to manifest in the numerator and denominator to cancel?
  17. Find the following limits using limit laws. If it is an indeterminate form of type $\dfrac{0}{0}$, make sure to properly deal with it.
    1. $\displaystyle\lim_{x\rightarrow 1} \sqrt{\dfrac{2x^2 + 2}{2x^2 - 1}}$
    2. $\displaystyle \lim_{x\rightarrow 5}\dfrac{x^2 - 6x + 5}{x - 5}$
    3. $\displaystyle \lim_{h\rightarrow 0}\dfrac{(4+h)^2 - 16}{h}$
    4. $\displaystyle \lim_{x\rightarrow 0}\dfrac{\sqrt{x^2 + 9} - 3}{x^2}$
    5. $\displaystyle \lim_{x\rightarrow 16}\dfrac{4 - \sqrt{x}}{16x - x^2}$
    6. $\displaystyle \lim_{x\rightarrow 0}\dfrac{1}{x} - \dfrac{1}{x^2 + x}$
      Hint: Subtract the two fractions first.
    7. $\displaystyle \lim_{t\rightarrow-3}\dfrac{t^2 - 9}{2t^2 + 7t +3}$
    8. $\displaystyle \lim_{h\rightarrow 0} \dfrac{\dfrac{1}{3 +h} - \dfrac{1}{3}}{h}$
  18. For the following problems, sketch the graph of $f$ and find $\displaystyle \lim_{x\rightarrow a} f(x)$, if it exists.
    1. $f(x) = \begin{cases} x^2 & x \leq 1 \\ x-1 & x > 1\end{cases}, \qquad a = 1$
    2. $f(x) = \begin{cases} x^2 - 3 & x \neq 0 \\ 0 & x = 0\end{cases}, \qquad a = 0$
    3. $f(x) = \begin{cases} -1 & x < 0 \\ x - 1 & x > 0 \end{cases}, \qquad a = 0$.
  19. Use the squeeze theorem to show \[\lim_{x\rightarrow 0}x^2 \cos (20\pi x) = 0\]
  20. If $ 4x - 9 \leq f(x) \leq x^2 - 4x + 7$ for all $x \geq 0$, find $\displaystyle\lim_{x\rightarrow 4}f(x)$.
  21. Given this graph of $f(x)$ Determine which statements are true or false.
    1. $\displaystyle\lim_{x\rightarrow 0^-} f(x) = 0$
    2. $\displaystyle\lim_{x\rightarrow 0^+} f(x) = 0$
    3. $f(1)$ is defined.
    4. $\displaystyle\lim_{x\rightarrow 2} f(x) = f(2)$
    5. $\displaystyle\lim_{x\rightarrow 1} f(x)= 1$
    6. $\displaystyle\lim_{x\rightarrow 3^-} f(x)= \lim_{x\rightarrow 3^+}f(x)$
    7. $f(x)$ is continuous from the right at $x = 1$.
  22. If a function $f(x)$ is continuous at $x = a$, what does $\displaystyle \lim_{x\rightarrow a} f(x)$ have to be?
  23. Suppose a function $f(x)$ has $f(2) = 5$ and $\displaystyle \lim_{x \rightarrow 2}f(x) = 5$. Is the function continuous at $x = 2$?
  24. In the context of finding a limit, why does continuity make the problem much easier?
  25. Use the three-part definition of continuity to explain why the function is continuous at the given number $a$.
    1. $\displaystyle f(x) = \begin{cases}(x-1)^2& x < 0 \\ (x+1)^2 & x \geq 0\end{cases} \qquad a = 0$
    2. $\displaystyle f(x) = \begin{cases}x(x-1)& x < 1 \\ 0 & x = 1 \\ \sqrt{x-1} & x > 1\end{cases} \qquad a = 1$
  26. Use the three-part definition of continuity to explain why the function is discontinuous at the given number $a$. Sketch the graph of the function.
    1. $\displaystyle f(x) = \begin{cases}x + 1 & x < 0 \\ x^2 & x \geq 0\end{cases} \qquad a = 0$
    2. $\displaystyle f(x) = \begin{cases}x + 5 & x < 0 \\ 2 & x = 0 \\ -x^2 + 5 & x > 0\end{cases} \qquad a = 0$
    3. $\displaystyle f(x) = \begin{cases}-x & x < 0 \\ 1 & x = 0 \\ x & x > 0\end{cases} \qquad a = 0$
  27. How would you define $f(2)$ in the function \[f(x) = \dfrac{x^2 - x - 2}{x - 2}\] in order to make $f(x)$ continuous at $x = 2$?
  28. Where is the function \[f(x) = \dfrac{\sin(x)}{(x^2 - 1)(x^2 - 4)}\] continuous?
  29. What's the difference between a removeable, jump and infinite discontinuity?
  30. Draw one graph of a function which satisfies the following conditions simultaneously:
    • Jump discontinuity at $2$ but continuous from the right at $2$
    • Discontinuous at $-1$ and $4$ but continuous from the left at $-1$ and from the right at $4$.
    • Continuous everywhere else
  31. Suppose you are asked to find the limit \[\lim_{x\rightarrow \pi} \dfrac{\sin^2(x)\cos^3(x)}{x^{52} - 4x^{49} + x^{32} - x^3 + x^2 + 44}\] You know the function is continuous at $x = \pi$. Find the limit.