Homework 6

Directions:

Show each step of your work and fully simplify each expression.
Turn in your answers in class on a physical piece of paper.
Staple multiple sheets together.
Feel free to use Desmos for graphing.

Answer the following:

A plane flying horizontally at an altitude of 1 mi and a speed of 500 mph passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 2 miles away from the station.
If the minute hand of a clock has length r (in centimeters) find the rate at which it sweeps out area as a function of r.
Use the equation of a sector of a circle $A = \dfrac{1}{2}r^2 \theta$ (picture showing this below) and the fact that the rate at which the minute hand moves is $2\pi$ radians per hour.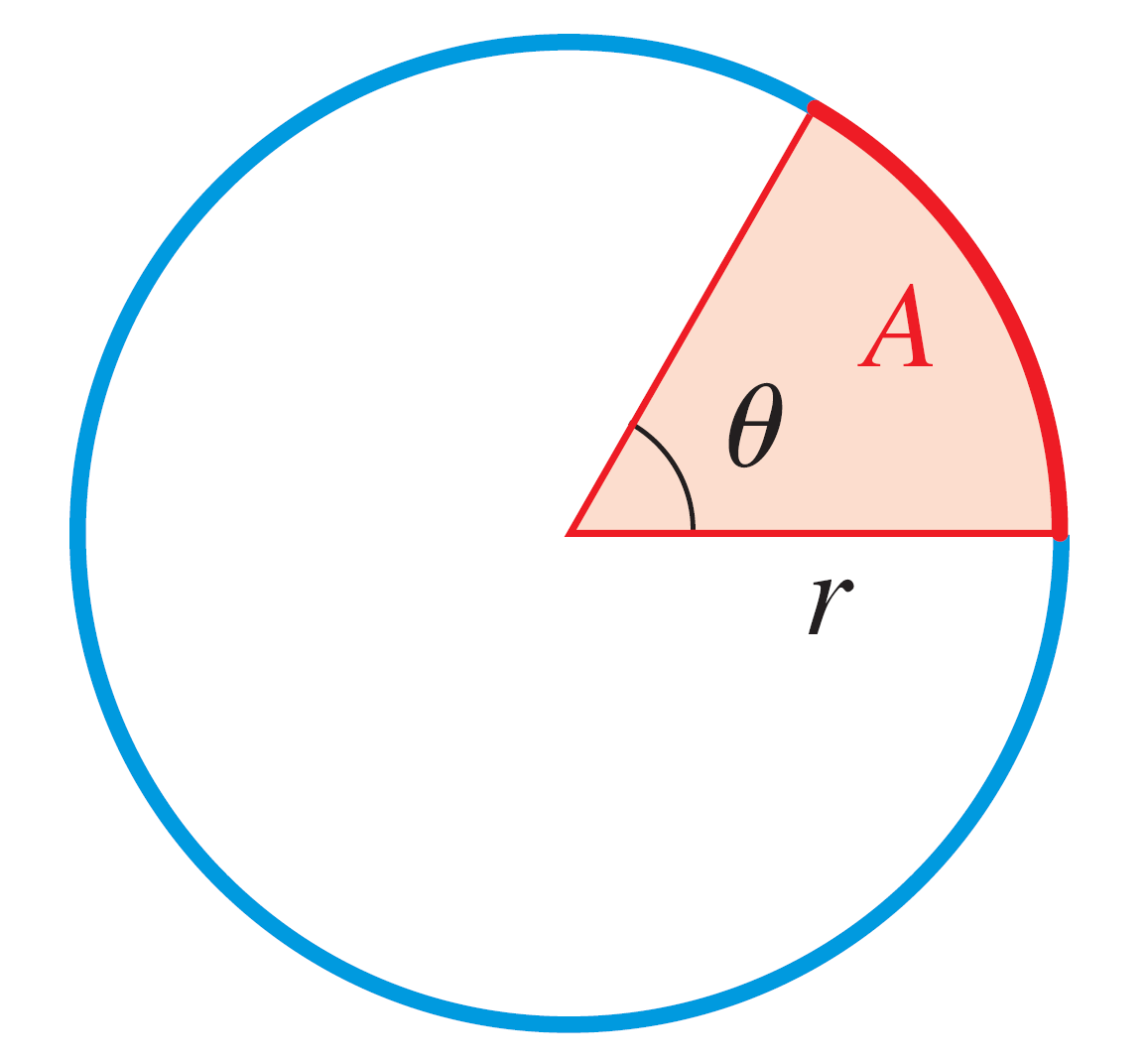
Suppose a meat distributor is willing to make $x$ pounds of beef available every week on the marketplace when the price is $\$p$ per pound. The relationship between quantity supplied $x$ and price $p$ is \[650p^2 - x^2 = 100\] If 30,000 pounds of beef are available on the marketplace this week and the price per pound is falling by 2 cents per week, at what rate is the supply falling?
Two resistors are connected in parallel, shown as follows 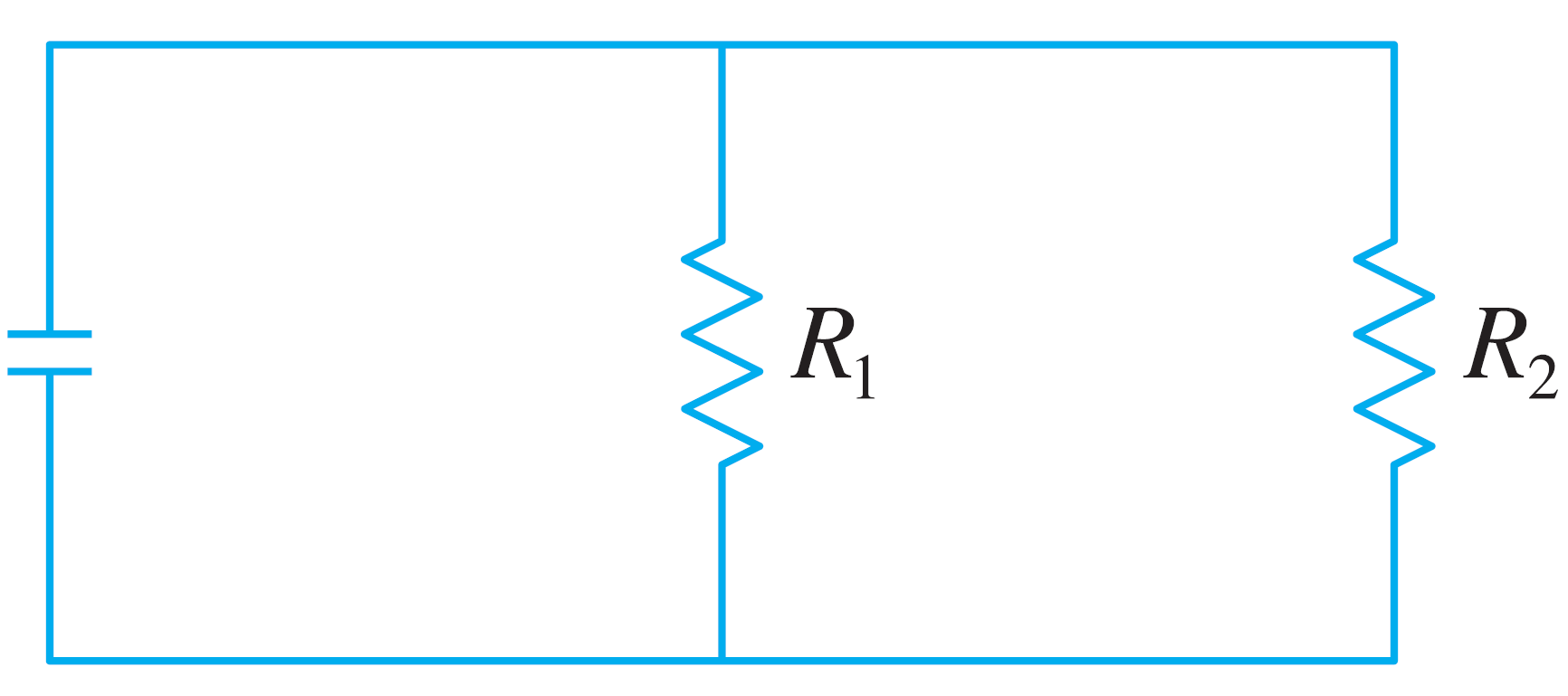The total resistance $R$, measured in ohms $\left(\Omega\right)$ is calculated by \[\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2}\] If $R_1$ is increasing $0.3\ \Omega$ per second and $R_2$ is increasing at $0.2\ \Omega$ per second, how fast is the total resistance $R$ changing when $R_1 = 80 \ \Omega$ and $R_2 = 100 \ \Omega$?
Hint: Do not make the most common mistake when solving RR problems.
A particle is moving along the curve of the equation $xy = 8$. As it reaches the point (4, 2), the $y$-coordinate is decreasing at a rate of 2 centimeters per second. How fast is the $x$-coordinate of the point changing at that instant?
Hint: Do not make the most common mistake when solving RR problems.
Find the linearization of the following functions at the $x$-coordinate $a$.
1. $f(x) = \sin x, \qquad a = 0$
2. $f(x) = \cos x, \qquad a = 0$
3. $f(x) = \sqrt{x}, \qquad a = 4$
4. $f(x) = 2x^2 - 1, \qquad a = 1$
Now approximate $\sin(0.01)$ and $\cos(-0.01)$ without a calculator.
Leibniz and prime notation for the derivative are equivalent: \[\dfrac{dy}{dx} = f'(x)\] Previously we said $\dfrac{dy}{dx}$ must be treated as one entity. In Section 2.9 what new interpretation of $dy$ and $dx$ do we have that allows us to treat $\dfrac{dy}{dx}$ like a fraction?
The following functions are in explicit form. Find the differential of the dependent variable.
1. $y = 2x^2 - 3$
2. $u = \sqrt{1 - x}$
3. $u = \sin\sqrt{t}$
4. $u = \dfrac{1}{x}\sin x$
5. $y = \tan (\pi x)$
6. $u = x^3$
Explain the difference between an absolute minimum and a local minimum.
If $f$ is a continuous function on $(a, b)$, must an absolute maximum exist?
Suppose $f(x)$ is continuous on $[a, b)$. Draw a graph of $f(x)$ where the absolute maximum cannot exist.
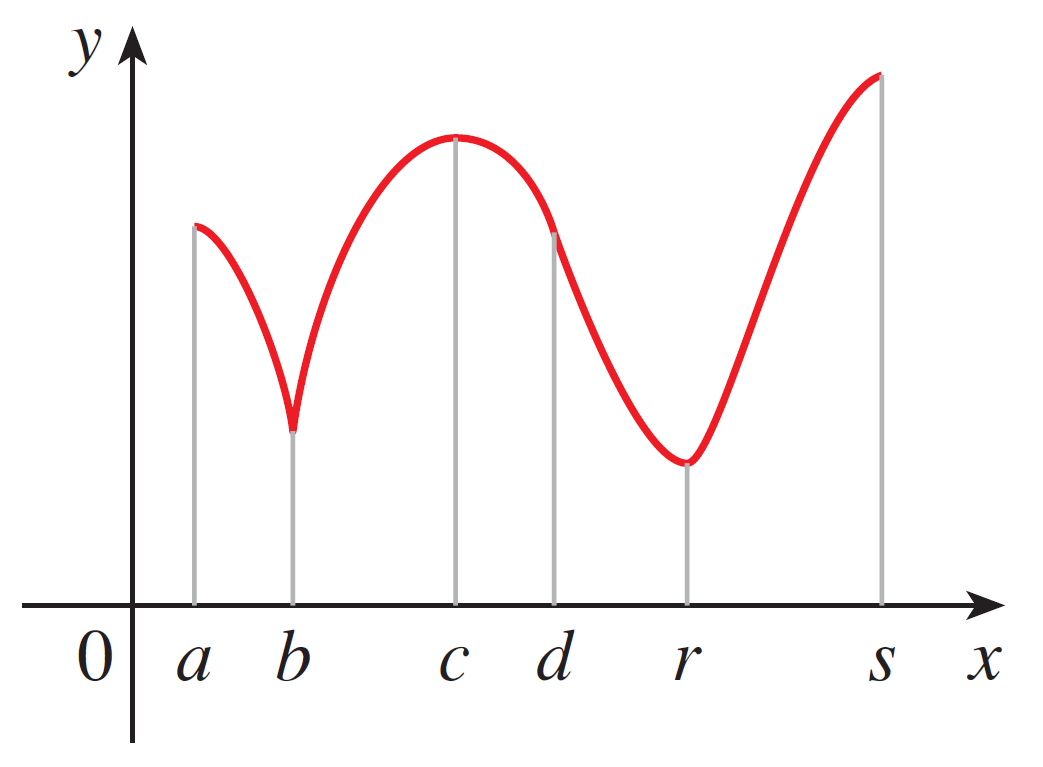
Identify all absolute/local minimums and maximums for the following function:
Draw a graph that is continuous on $[-2, 5]$ and has absolute minimum at $x = 3$, absolute maximum at $x = 0$.
Draw one graph that meets the following criteria:
1. Domain of $\mathbb{R}$
2. Local maximums $f(2) = -2, \ f(-3) = -1$
3. Local minimums $f(-1) = 3, \ f(-2) = 0$
4. Differentiable on $(-\infty, 2) \cup (2, \infty)$
State the definition of a critical number of a function $f$.
From a problem-solving perspective, without using the mathematical definition of a critical number, what does the critical number of a function tell us about?
Find the critical numbers for the following functions:
1. $f(x) = x^3 + 6x^2 - 15x$
2. $f(t) = t^4 + t^3 + t^2 + 1$
3. $f(y) = \dfrac{y - 1}{y^2 - y + 1}$
4. $f(x) = \sqrt{1 - x^2}$
Find the absolute maximum and minimum for the following functions:
1. $f(x) = 12 + 4x - x^2, \qquad [0, 5]$
2. $f(x) = x^3 - 6x^2 + 5, \qquad [-3, 5]$
3. $f(t) = (t^2 - 4)^3, \qquad [-2, 3]$
4. $f(x) = x + \dfrac{1}{x} \qquad \left[\frac{1}{5}, 4\right]$
5. $f(x) = 5 + 54x - 2x^3, \qquad [0, 4]$
6. $f(x) = \sin x, \qquad [-2\pi, 2\pi]$
If $a$ and $b$ are positive numbers, find the global maximum value of \[f(x) = x^a(1-x)^b, \qquad 0 \leq x \leq 1\]

Hint 1: Take the derivative, factor out $x^{a-1}(1-x)^{b-1}$, and use the zero product property on each factor.
Hint 2: The solution is one fraction with $a$ in the numerator and $a$'s and $b$'s in the denominator.
Cool fact: the above function is related to a statistical distribution called the Beta distribution. You just found the average of this distribution!
When using Rolle's Theorem or the Mean Value Theorem, what do you need to check first before using them?
Verify the function \[f(x) = 2x^2 - 4x + 5 \] satisfies the three hypotheses of Rolle's Theorem on the interval $[-1, 3]$. Then find all numbers $c$ that satisfy the conclusion of Rolle's Theorem.
Verify the function \[f(x) = x + \dfrac{1}{x} \] satisfies the three hypotheses of Rolle's Theorem on the interval $\left[\dfrac{1}{2}, 2\right]$. Then find all numbers $c$ that satisfy the conclusion of Rolle's Theorem.
Using English, describe the intuition behind the Mean Value Theorem.
For the following functions, find the number $c$ that satisfies the conclusion of the Mean Value Theorem on the given interval.
1. $f(x) = \sqrt{x}, \ [0, 4]$
2. $f(x) = x^3 - 2x, \ [-2, 2]$
Suppose $f(x) = 1 - x^{2/3}$. Show $f(-1) = f(1)$ but there is no $c \in (-1, 1)$ where $f'(c) = 0$. Why does this not contradict Rolle's Theorem?
Hint: Differentiability was violated somewhere. Find where $f'(x)$ DNE.
Suppose that $f$ is continuous on $[a, b]$. Must there be a number $c \in (a, b)$ where \[f'(c) = \dfrac{f(b) - f(a)}{b - a}\] If not, draw a graph in which such a $c$ cannot exist.
(skip this) Suppose two functions $f(x)$ and $g(x)$ satisfy the equation \[f'(x) = g'(x)\]
1. Algebraically speaking, what is the relationship between $f(x)$ and $g(x)$?
2. Geometrically speaking (using the graph), what is the relationship between $f(x)$ and $g(x)$?