Homework 8

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

  1. Find the limit or show it does not exist:
    1. $\displaystyle \lim_{x\rightarrow \infty} \dfrac{3x - 2}{2x + 1}$
    2. $\displaystyle \lim_{x\rightarrow -\infty} \dfrac{4x^3 + 6x^2 - 2}{2x^3 - 4x + 5}$
    3. $\displaystyle \lim_{x\rightarrow \infty} \cos(x)$
    4. $\displaystyle \lim_{x\rightarrow \infty} (\sqrt{9x^2 + x } - 3x)$
    5. $\displaystyle \lim_{x\rightarrow \infty} \dfrac{x^2}{\sqrt{x^4 + 1}}$
    6. $\displaystyle \lim_{x\rightarrow \infty} \dfrac{x}{x^2 + 1}$
    7. $\displaystyle \lim_{x\rightarrow \infty} \dfrac{\sqrt{1 + 4x^6}}{2 - x^3}$
    8. $\displaystyle \lim_{x\rightarrow \infty} (x^2 - x^4)$
    9. $\displaystyle \lim_{x\rightarrow \infty} (\sqrt{x} - x)$
  2. Sketch a graph of the function which satisfies the following:
    • $f'(2) = 0, \ f(2) = -1, \ f(0) = 0$
    • $f'(x) < 0$ when $0 < x < 2$
    • $f'(x) > 0$ when $ x > 2$
    • $f''(x) < 0$ when $0 < x < 1$ or $x > 4$
    • $f''(x) > 0$ when $1 < x < 4$
    • $\displaystyle \lim_{x\rightarrow \infty} f(x) = 1$
  3. Think of three examples in your life in which you want to find an absolute maximum.
  4. You want to create a rectangle with 200 meters perimeter. Using calculus, what dimensions maximize the area?
  5. You take two shots of vodka. Your Blood Alcohol Content (BAC) is estimated by the function \[f(t) = \dfrac{1}{10} \cdot \dfrac{t}{1 + t^2} , \quad t > 0\] where $f(t)$ is measured in grams/100 mL (same unit as %) and $t$ is tens of minutes. For example, $t = 3$ is 30 minutes.

    Using calculus, find the time where you reach maximum BAC and the value of BAC.

  6. Suppose someone owns 4000 meters of fencing. They wish to create a rectangular piece of grazing land where one side is along a river. This means no fence is needed for that side. Moreover, they wish to subdivide the rectangle into three separate sections with two pieces of fence, both of which are parallel to the sides not along the river. What are the dimensions of the largest area that can be enclosed?
  7. Consider the line $y = 3x- 2$. Find the point on the line that is the closest to the origin $(0, 0)$.

    Hint: Distance formula between two points.

  8. You have a circle of radius 2 and a rectangle with undetermined side lengths. Find the area of the largest rectangle that can be fully inscribed in the circle.

    Hint: Inscribed means all four vertices of the rectangle are touching the edge of the circle.

  9. Consider the function \[f(x) = 9x-2x^{3}+\frac{1}{5}x^{5}, \qquad x \in \left[-\sqrt{3}, \sqrt{3}\right]\] Find the $x$-coordinate(s) where the tangent lines have the maximal slope.
  10. Suppose you have two positive numbers $x$ and $y$. Find the values of $x$ and $y$ where their sum is 18 and their product is maximized.
  11. Suppose you have two functions \[f(x) = (x+1)^2 \qquad \qquad g(x) = -x^2\] What is the minimum vertical distance between the two functions?

    Hint: Take the difference of the two functions. This expression represents the vertical distance between the two functions. But be careful! The function with the larger $y$-coordinates should be on the left of the subtraction.

  12. Suppose the product of two positive numbers is 100. Find the two numbers that minimize the sum.
  13. Suppose $f(x) = x^2$ and consider the point $(3, 0)$.
    1. Find the point $P$ on the graph of $f(x)$ that minimizes the distance between $P$ and $(3, 0)$.
    2. Now for the point $P$, find the equation of the normal line.
    3. Graph $f(x)$, the point $P$ and the normal line in Desmos. What do you notice about the relationship between $P$ and the normal line?
    4. Given part (c), complete this sentence: "It seems like the shortest distance between a curve and a point will be $\dots$".
  14. Suppose two functions $f(x)$ and $g(x)$ satisfy the equation \[f'(x) = g'(x)\]
    1. Algebraically speaking, what is the relationship between $f(x)$ and $g(x)$?
    2. Geometrically speaking (using the graph), what is the relationship between $f(x)$ and $g(x)$?
  15. If $f(x)$ is a function, what is true about the antiderivative $F(x)$?
  16. If $f(x) = 3x^3$, is $g(x) = 9x^2$ an antiderivative of $f(x)$? How about $h(x) = x^4$?
  17. Suppose $f(x) = x^4$. Find three different antiderivatives $F_1(x), F_2(x)$ and $F_3(x)$ of $f(x)$.
  18. Find the most general antiderivative of the following functions:
    1. $f(x) = 5$
    2. $f(x) = x$
    3. $f(x) = \sqrt{x}$
    4. $f(x) = \dfrac{2}{\sqrt{x^3}}$
    5. $f(x) = x^2x^{-9/2}$
    6. $f(x) = 4x + 7$
    7. $f(x) = 3\cos x - 4 \sin x$
    8. $f(x) = x(x-1)$
    9. $f(x) = \dfrac{10}{x^9}$
    10. $g(\theta) = -\sec^2 \theta$
    11. $f(x) = 6x^5 - 8x^4 - 9x^2$
    12. $f(x) = \sqrt{x} - 3\sqrt[4]{x^3}$
    13. $f(x) = 3\cos x - \sec x \tan x$

    19. The rest of these problems will appear on next week's homework. Skip the rest of these for this homework.

  19. Find the function $f(x)$.
    1. $f'(x) = 1 + 3\sqrt{x}, \qquad f(4) = 25$
    2. $f'(x) = x, \qquad f(2) = 3$
    3. $f''(x) = -12x^2 + 12x - 2, \qquad f(0) = 4, \qquad f'(0) = 12$
    4. $f''(x) = 8x^3 + 5, \qquad f(1) = 0, \qquad f'(1) = 8$
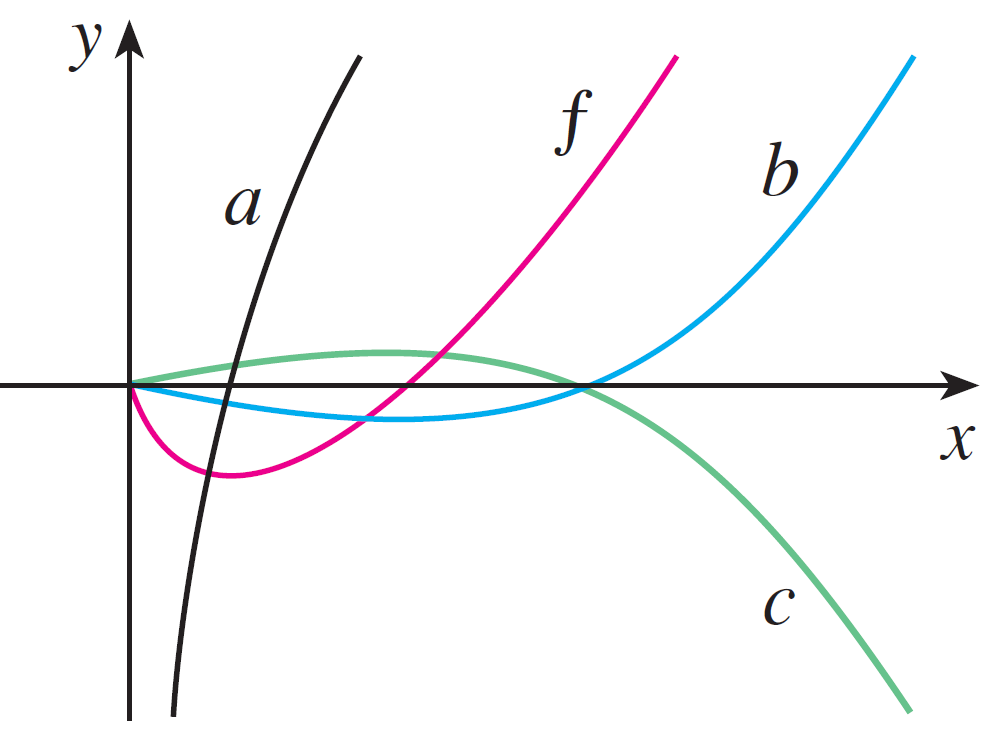
  20. A graph of $f(x)$ is given. Is $a$, $b$, or $c$ the antiderivative of $f(x)$?