Homework 9

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

  1. Find the most general antiderivative of \[f(x) = \dfrac{2}{\sqrt{x^3}} - \sec x \tan x + \sin^2 x + \cos^2 x\]
    Hint: Pythagorean Identity for trigonometry.
  2. Antiderivatives undo what the derivative did! We know how to undo the power rule: \[\text{if } f(x) = x^n, \text{ then } F(x) = \dfrac{x^{n+1}}{n+1}\] We will need to undo the Product, Quotient, and Chain Rules!
    Question: Suppose $f(x) = \cos(x^2)\cdot 2x$. What is the antiderivative $F(x)$?
    Think of what derivative rule you need to undo.
  3. Find the function $f(x)$.
    1. $f'(x) = 1 + 3\sqrt{x}, \qquad f(4) = 25$
    2. $f'(x) = x, \qquad f(2) = 3$
    3. $f''(x) = -12x^2 + 12x - 2, \qquad f(0) = 4, \qquad f'(0) = 12$
    4. $f''(x) = 8x^3 + 5, \qquad f(1) = 0, \qquad f'(1) = 8$
  4. A graph of $f(x)$ is given. Is $a$, $b$, or $c$ the antiderivative of $f(x)$?
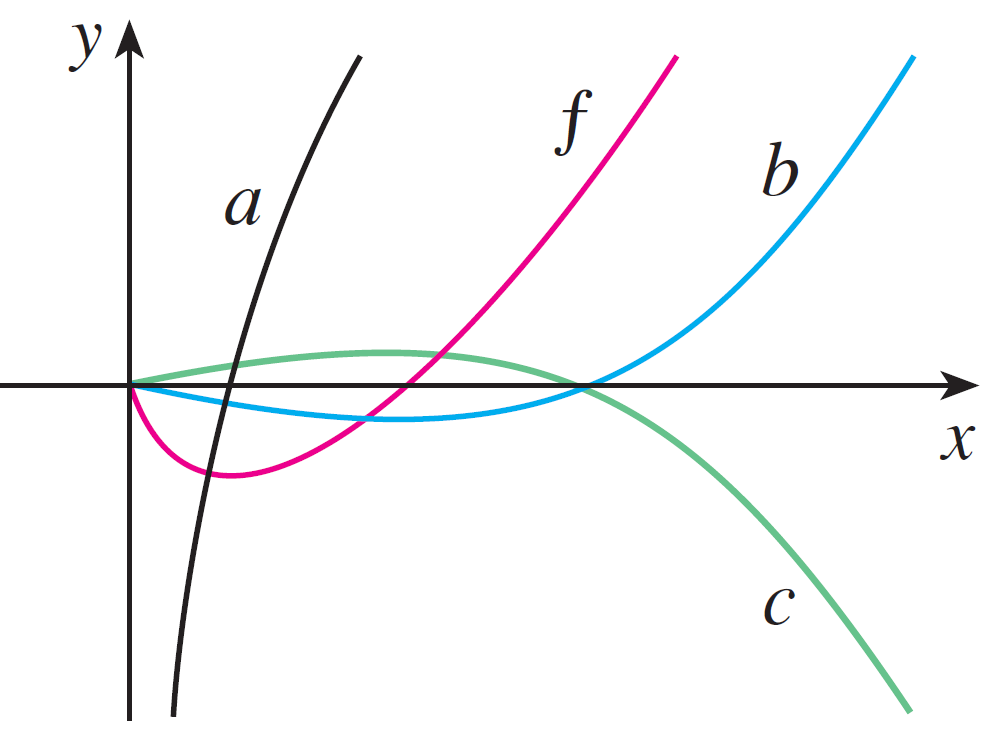
  5. Evaluate the following sums:
    1. $\displaystyle\sum^5_{i=1}\left[i - 1\right]$
    2. Given that $f(x) = x^2$, calculate $\displaystyle\sum^5_{i=1}f(i)$
    3. $\displaystyle\sum^4_{n=1} n(n-1)$
    4. $\displaystyle\sum^8_{n=2}\left(\dfrac{1}{n} - \dfrac{1}{n + 1}\right)$
      • Hint: Look for a pattern that helps you cancel! This concept is called a telescoping series, which you will use in Calculus III.
    5. Given that $f(x) = \dfrac{1}{x + 1}$, calculate $\displaystyle\sum^5_{i=1}\left(f(i) - f(i-1)\right)$
    6. $\displaystyle\sum^{100}_{n=1} (-1)^n(n+2)$
      • Hint: Look at each pair of terms (1st + 2nd, 3rd + 4th, etc). How many such pairs are there?
  6. What is the Distance problem in Calculus? How about the Area problem?
  7. Approximate the area underneath the graph of $f(x) = \sin x$ on $\left[0, \frac{\pi}{2}\right]$ by using four rectangles and right endpoints.
    Only set up the sum; do not find the actual number. Unless you want to practice using Half-Angle Formulas!
  8. Approximate the area underneath the graph of $f(x) = \dfrac{1}{x}$ on $\left[1, 2\right]$ by using four rectangles and right endpoints.
    Only set up the sum; do not find the actual number.
  9. Approximate the area underneath the graph of $f(x) = x^3$ on $\left[0, 1\right]$ by using eight rectangles and right endpoints.
    Only set up the sum; do not find the actual number.
  10. To find the area underneath the curve of $f(x)$ on the interval $[a, b]$, without using the integral symbol, what is the exact formula for this area?
  11. In the context of finding the area underneath the curve, explain what each of the parts of the formula is describing:
    1. The $f(x_i) \cdot \Delta x$
    2. The $\displaystyle\sum^{n}_{i=1}$
    3. The $\displaystyle\lim_{n\rightarrow \infty}$
  12. If $\displaystyle \int^{5}_{-5} f(x) \ dx = 12$ and $\displaystyle \int^1_{-5} f(x) \ dx = 3$, find $\displaystyle \int^{5}_{1} f(x) \ dx$.
  13. We saw from lecture that \[\int^1_0 x^2 \ dx = \dfrac{1}{3}\] What is $\displaystyle\int^0_1 x^2 \ dx$?
  14. If $\displaystyle \int^{8}_0 f(x) \ dx = 3$ and $\displaystyle \int^0_{-3} f(x) \ dx = 4$, what is $\displaystyle \int^8_{-3} f(x) \ dx$?
  15. If $\displaystyle \int^4_2 f(x) \ dx = 3$ and $\displaystyle \int^4_2 g(x) \ dx = -2$, evaluate the following integrals
    1. $\displaystyle \int^4_2 [f(x) + g(x)] \ dx$
    2. $\displaystyle \int^4_2 [f(x) - g(x)] \ dx$
  16. Describe in English what the Fundamental Theorem of Calculus Part 1 is saying.
  17. Find the derivative of the following functions:
    1. $g(x) = \displaystyle \int^x_0 \sqrt{t + t^3} \ dt$
    2. $g(x) = \displaystyle \int^x_0 \sin(t^2) \ dt$
    3. $F(x) = \displaystyle \int^0_x \sqrt{t^3} \ dt$
      Hint: Property 6 of Definite Integrals.
  18. In English, what does FTC Part 2 tell us about how to find definite integrals?
  19. If $f(x) = x - 1$, what does the expression \[f(x) \bigg\rvert^1_{-1}\] evaluate to?
    Hint: beware of the common mistake (forgetting parentheses).
  20. Evaluate the following integrals using FTC Part 2:
    Hint: If you are struggling to find the antiderivative, simplify first!
    1. $\displaystyle \int^5_{-5} 3 \ dx$
    2. $\displaystyle \int^1_0x^2 \ dx$
    3. $\displaystyle \int^3_1(x^2 + 2x - 4) \ dx$
    4. $\displaystyle \int^\pi_{\pi/6} \sin \theta \ d\theta$
    5. $\displaystyle \int^1_0 (x-1)(x+1) \ dx$
    6. $\displaystyle \int^{\pi/3}_{\pi/6} \sec^2 x\ dx$
    7. $\displaystyle \int^{2}_{1} \left(3x^2 + x\right) \ dx$
    8. $\displaystyle \int^{2}_{0} \dfrac{x^2 - 1}{x + 1} \ dx$
    9. $\displaystyle \int^{2}_{0} \dfrac{2x^2 - 7x + 3}{4x - 2} \ dx$
    10. $\displaystyle \int_{-2}^0 2 \ dx + \int^2_0 (4 - x^2) \ dx$
  21. Find the area enclosed between the curve and the $x$-axis of the function $y = \sqrt{x}$ on the interval $[0, 4]$.
  22. (skip this) Why can't you use FTC to find this integral? \[\int^2_{-2} \dfrac{1}{x} \ dx\]