3.1: Maximum and Minimum Values

Chapter 3 has two goals:

Understand how we can use the derivative.

Prepare for understanding the integral, a core concept in Calculus II.

Some of the most important applications of differential calculus are optimization problems, in which we are required to find the optimal (best) way of doing something. For example:

What is the shape of a can that minimizes manufacturing costs?
In GPT-3, how can we "minimize error" so that GPT sounds like real English?

Let's dive into exploring how to find minimum and maximums.

Absolute and Local Extreme Values

Let $c$ be in the domain $D$ of $f(x)$. Then $f(c)$ is the

absolute maximum value of $f$ if $f(c) \geq f(x)$ for all $x \in D$ and
absolute minimum value of $f$ if $f(c) \leq f(x)$ for all $x \in D$.

The comparison above was with all numbers in the domain. We can restrict our context to just be near a point instead.

The number $f(c)$ is a

local maximum value of $f$ if $f(c) \geq f(x)$ when $x$ is near $c$ and
local minimum value of $f$ if $f(c) \leq f(x)$ when $x$ is near $c$.

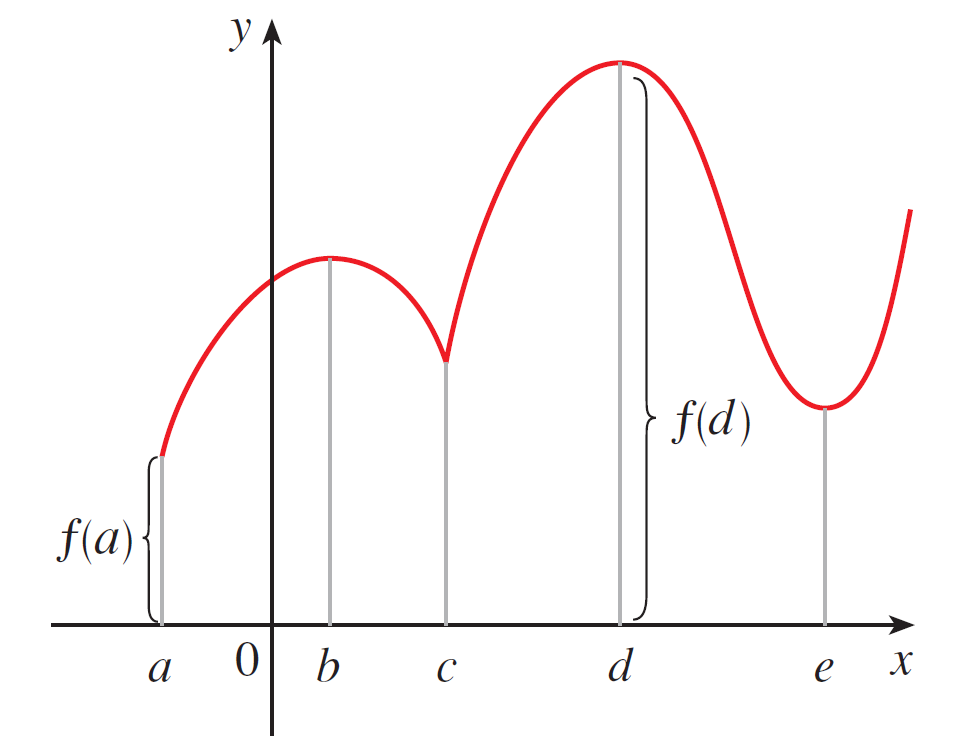
Identify all absolute/local minimums and maximums for the following function:

Identify all absolute/local minimums and maximums for $f(x) = x^2$ and $f(x) = x^3$.

When do absolute extrema exist? Turns out you only need two requirements.

The Extreme Value Theorem
If $f$ is continuous on a closed interval $[a, b]$, then $f$ is guaranteed to have an absolute maximum $f(c)$ and an absolute minimum $f(d)$ for some $c,d \in [a, b]$.

*pictures in class*

The Closed Interval Method

We are interested in locating where the absolute minimum/maximum occur.

These graphs show absolute min/max can occur at a local min/max or an endpoint.

If it is at a local min/max, then either $f'(c) = 0$ or there is a corner at $c$, meaning $f'(c)$ does not exist. Such numbers are given a name:

A critical number of $f$ is a number $c$ where $f'(c) = 0$ or $f'(c)$ does not exist.

Find all critical numbers of $f(x) = x^{3/5}(4 - x)$.

Find all critical numbers $f(x) = x^3 + 3x^2 - 24x$.

The Closed Interval Method
To find the absolute maximum and minimum values of a continuous function $f$ on a closed interval $[a, b]$:

Find the values of $f$ at the critical numbers of $f$ in $(a, b)$.
Find the values of $f$ at the endpoints of the interval.
The largest number from Steps 1 and 2 is the absolute maximum and the smallest is the absolute minimum.

Find the absolute extrema of the function \[f(x) = x^3 - 2x^2 - 4x + 4\] on $[0, 3]$.

Find the absolute extrema of \[f(x) = x^{2/3}\] on $[-1, 8]$.