Homework 10
Directions:
- Show each step of your work and fully simplify each expression.
- Turn in your answers in class on a physical piece of paper.
- Staple multiple sheets together.
- Feel free to use Desmos for graphing.
Answer the following:
- If the minute hand of a clock has length r (in centimeters) find the rate at which it sweeps out area as a function of r.
Hint: Use the equation of a sector of a circle $A = \dfrac{1}{2}r^2 \theta$ (picture showing this below) and the fact that the rate at which the minute hand moves is $2\pi$ radians per hour.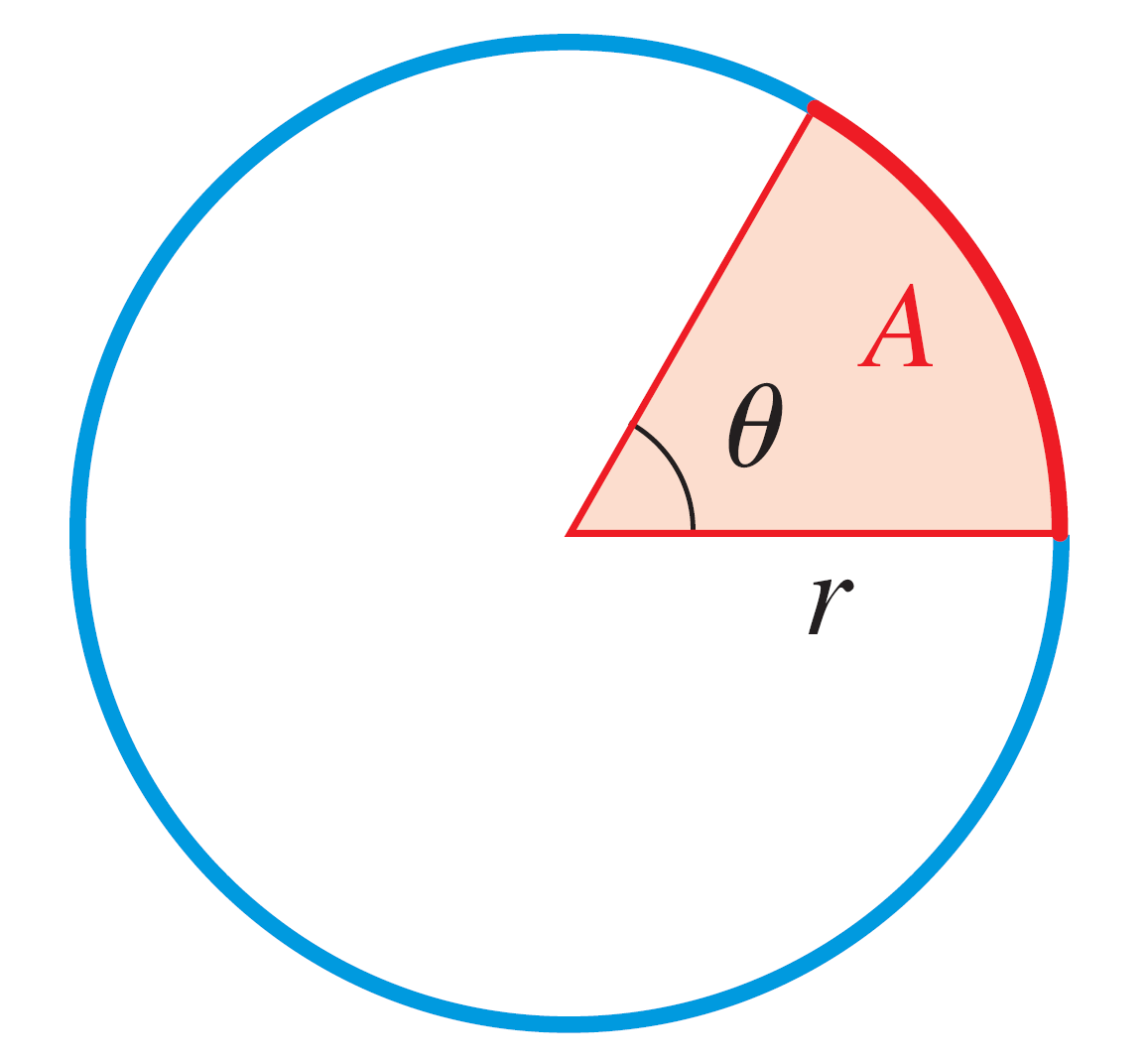
- Suppose a meat distributor is willing to make $x$ pounds of beef available every week on the marketplace when the price is $\$p$ per pound. The relationship between quantity supplied $x$ and price $p$ is \[650p^2 - x^2 = 100\] If 30,000 pounds of beef are available on the marketplace this week and the price per pound is falling by 2 cents per week, at what rate is the supply falling?
Hint: the quantity supplied $x$ and the price per pound $p$ are quantities that change every week, or in other words, over time.
- Differentiate the following. Remember you can use logarithmic differentiation to simplify the form for some problems.
- $f(x) = x\ln x$
- $f(x) = \log_3(1-x)$
- $f(x) = \ln (\sin^2 x)$
- $f(x) = \sqrt[5]{\ln x}$
- $f(x) = \ln{\sqrt[5]{x}}$
- $y = \ln(e^{-x} + xe^{-x})$
- $y = \dfrac{\sin x \cos^2 x}{(x^2 + 1)^4}$
- $f(x) = x\ln x$
- $f(x) = x^{\cos x}$
- $f(x) = x^{x}$
- $f(x) = (\sin x)^{\sin x}$
- $f(x) = \sqrt{x} \cdot e^{x^2} \cdot (x^2 -1)^3$
- Find the linearization $L(x)$ of the following functions at the given number $a$.
- $f(x) = x^4 + 3x^2$ at $a = -1$
- $f(x) = \cos x$ at $a = \dfrac{\pi}{2}$
- Find the Taylor polynomial of degree 3 at $a = 0$ for $f(x) = \sin \pi x$.
- Find the Taylor polynomial of degree 4 at $a = 1$ for $f(x) = \dfrac{1}{x}$.
- Find the Taylor polynomial of degree 2 at $a=4$ for $f(x) = \sqrt{x}$.