Homework 3

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

  1. Suppose $f(x) = 2^x$. Evaluate the following; your answer must be one singular number with no exponents.
    1. $f(-1)$
    2. $f(0)$
    3. $\sqrt[3]{f(6)}$
    4. $f(5)$
  2. You are given a function $F(x)$. Find two functions $f, g$ where $F = f \circ g$.
    1. $F(x) = e^{\sin(x)}$
    2. $F(x) = \sin(10^x)$
    3. $F(x) = \log_{32}(e^x)$
    4. $F(x) = e^{5x}$
    5. $F(x) = (e^x)^4$
    6. $F(x) = \ln(\sin(x))$
  3. Draw two graphs of two functions, one of which is not one-to-one and one of which is one-to-one.
  4. For each of the following functions, determine if they are inverses of each other.
    1. $f(x) = 2x - 1, \ \ g(x) = \dfrac{x + 1}{2}$
    2. $f(x) = \dfrac{1}{x}, \ \ g(x) = \dfrac{1}{x}$
    3. $f(x) = \dfrac{1}{x - 1}, \ \ g(x) = x + 1$
    4. $f(x) = \log_{5}(x), \ \ g(x) = 5^x$
    5. $f(x) = e^\sqrt{x}, \ \ g(x) = (\ln(x))^2$
  5. If $f$ is a one-to-one function and $f(6) = 17$, what is $f^{-1}(17)$?
  6. Show why $f^{-1}$ is not the same function as $\dfrac{1}{f}$ with an example.
    Hint: The function $f(x) = x^2$. Find $\dfrac{1}{f(x)}$ and use the inverse function property.
  7. Combine into one logarithm:
    1. $2 \ln 5 + 3 \ln 2$
    2. $3\log_{10}(a + b) - \frac{1}{2}\log_{10}(a-b) - 2\log_{10}c$
    3. $\ln(a + b) - \ln(a-b) - 2\ln c$
  8. Solve each equation for $x$:
    1. $\ln(x^2 - 1) = 3$
    2. $e^{2x}-5e^x + 4 = 0$
      Hint: Let $y = e^x$, and perform substitution described in Lecture Note III.
    3. $2^{x-5}=3$
    4. $\ln(3x - 10) = 2$
  9. List the first five terms of these sequences. Make sure you have a list of numbers.
    1. $a_n = \dfrac{1}{n^2}$
    2. $a_n =(-1)^{n+1}2^n$
    3. $a_n = \dfrac{2n}{n^2 + 1}$
    4. $a_n = \cos\dfrac{n\pi}{2}$
  10. Find a formula for $a_n$ for the following sequences:
    1. $1, 0, -1,0, 1, 0, -1, 0, \dots$
    2. $\dfrac{1}{2}, -\dfrac{4}{3}, \dfrac{9}{4}, - \dfrac{16}{5}, \dfrac{25}{6}, \dots$
    3. $-1, 2, -4, 8, -16, 32, \dots$
  11. Draw a graph of a sequence which satisfies \[\lim_{n\rightarrow \infty} a_n = 3\]
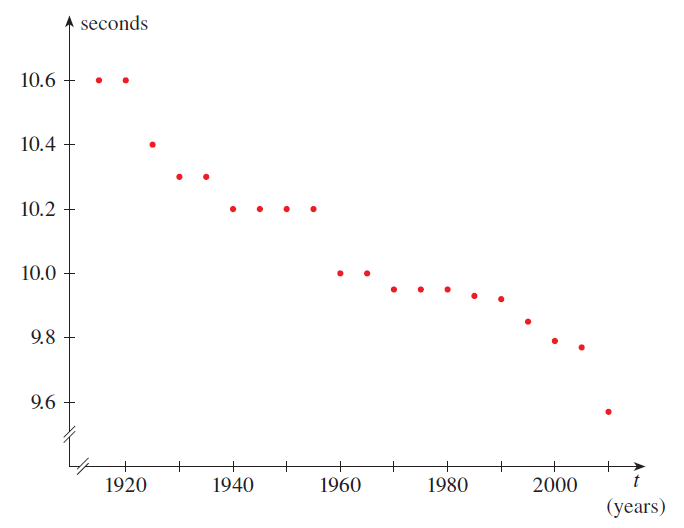
  12. Below is a sequence $a_t$ of the world record times for the men's 100 meter spring every five years.
    • From a biological perspective, do you think $\lim_{t\rightarrow\infty} a_t = 0$ or greater than zero? Justify your answer.
  13. Determine whether the following sequences are convergent or divergent. For the ones that converge, find out what it converges to.
    1. $a_n = \dfrac{3 + 5n}{2 + 7n}$
    2. (skip this one) $a_n = 2^{-n} + 6^{-n}$
    3. (skip this one) $a_n = \dfrac{10^n}{1 + 9^n}$
    4. (skip this one) $a_n = \dfrac{3^{n+2}}{5^n}$
    5. $a_n = \dfrac{2n^3 + n - 1}{n^2 + 1}$
    6. (skip this one) $a_n = \dfrac{2^n + 3^n}{5^n}$
    7. (skip this one) $a_n = \dfrac{n^3}{\sqrt{n^7 + 1}}$