Homework 8

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

  1. Find the derivative of each of the following functions. Remember to recognize the form, whether it be factors, composition, etc.
    1. $y = \dfrac{x^2 + 1}{x^2 - 1}$
    2. $y = \dfrac{1 + 2x}{3 - 4x}$
    3. $f(x) = \dfrac{x}{x + \frac{1}{x}}$
    4. $f(x) = \sec x$
    5. $f(x) = \cot x$
    6. $f(x) = \dfrac{\sec x}{1 + \tan x}$
    7. $f(t) = e^t\sin t$
    8. $f(x) = (x^4 + 4x^2)e^x$
    9. $y = \dfrac{e^x}{1 + x}$
    10. $f(t) = \dfrac{t - \sqrt{t}}{t^{1/3}}$
    11. $y = e^{\sqrt{x}}$
    12. $f(x) = (3x - x^3)^{23}$
    13. $f(x) = \sqrt[3]{1 + \tan x}$
    14. $f(x) = xe^{-2x}$
    15. $f(x) = (3x + 2)^3(4x^2 + 3)^4$
    16. $y = \sqrt{x + \sqrt{ x + \sqrt{x}}}$
    17. $f(x) = 2^{\sin \pi x}$
    18. $f(x) = \sqrt{\dfrac{x}{x^2 + 4}}$
    19. $f(x) = e^{e^x}$
    20. $f(x) = \sin x + \sin^2 x$
    21. $f(x) = 2^{3^x}
  2. Find the equation of the tangent line to the curve at the given point.
    1. $y = (1 + 2x)^{10}, \qquad (0, 1)$
    2. $y = \sin(\sin(x)), \qquad (\pi, 0)$

    3. The rest of these problems will appear on next week's homework. Skip the rest of these for this Homework.

  3. What is the main intuition behind implicit differentiation?
  4. Isolate $z$ in the equation \[-\sin(xy)(x + xz) = 1 + \cos(y)z\]
  5. Find $dy/dx$ with implicit differentiation for the equation \[x^3 + y^3 + x^2 + y = 1\]
  6. Consider the equation $x^{2/3} + y^{2/3} = 4$. Find the equation of the tangent line at the point $(-3\sqrt{3}, 1)$.
  7. Given an equation in implicit form, should you manipulate the equation before applying the derivative to both sides?
  8. Here is the curve of $x^3 + y^3 = 6xy$: 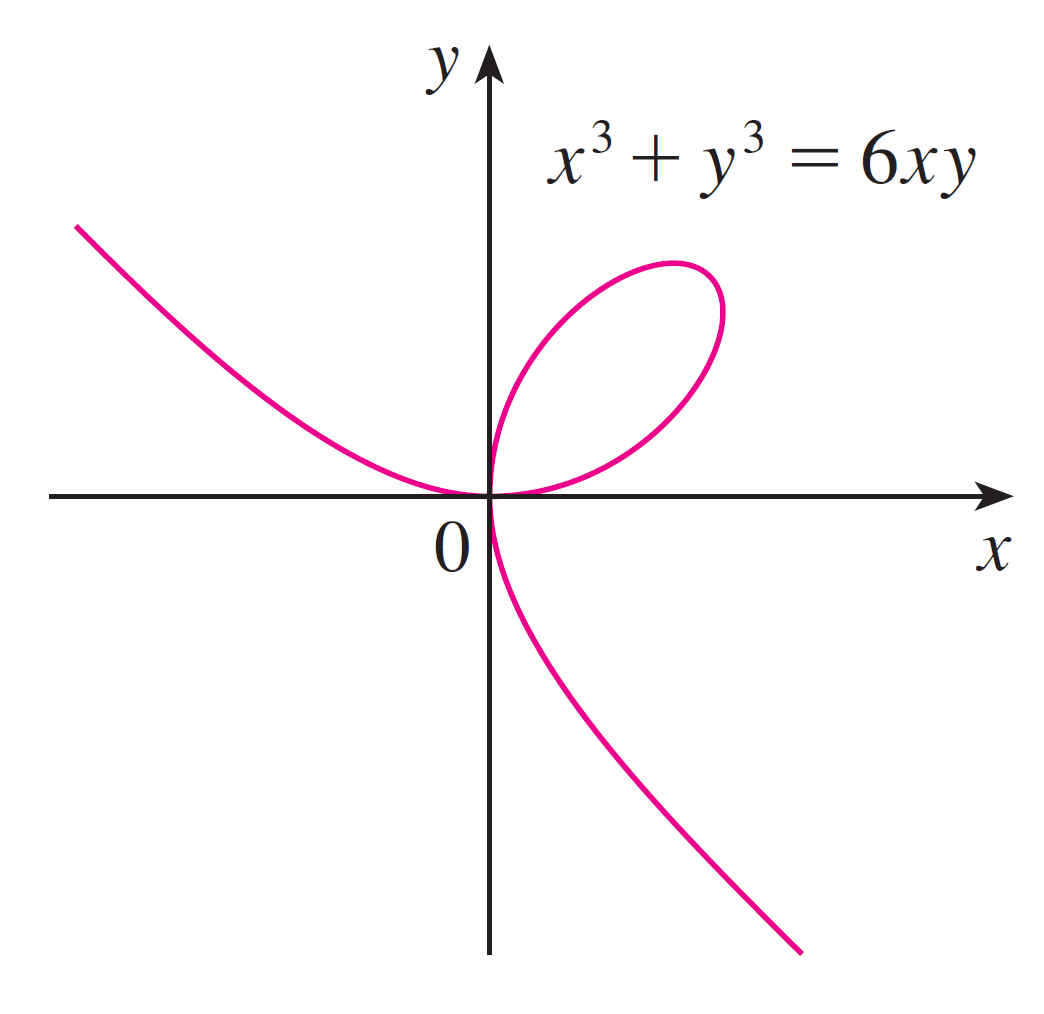In implicit differentiation, we assume $y = f(x)$ under suitable conditions. Draw multiple graphs which represent these "suitable conditions.". Hint: Chop up the curve so each part passes the vertical line test.
  9. Find $dy/dx$ with implicit differentiation:
    1. $x^2 - xy - y^2 = 4$
    2. $1 + x = \sin(xy)$
    3. $x^4y^3 + x^2y^4 = 2$
    4. $2\sqrt{x} + \sqrt{y} = 3$
    5. $(x + y)^3 + x^3 + y^3 = 0$
    6. $\dfrac{x}{y^3 - y} = 1$
    7. $\sin(x + y) = y^2 \cos x$
    8. $(x+y)^3 + x^3 + y^3 = 0$
  10. Find the equation of the tangent line at $(1,2)$ for the equation \[x^2 + 2xy - y^2 + x = 2\]
  11. Find the equation of the tangent line at $(\pi, \pi)$ for the equation \[\sin(x + y) = 2x - 2y\]