Homework 9

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

  1. What is the main idea behind implicit differentiation?
  2. Isolate $z$ in the equation \[-\sin(xy)(x + xz) = 1 + \cos(y)z\]
  3. Find $dy/dx$ with implicit differentiation for the equation \[x^3 + y^3 + x^2 + y = 1\]
  4. Consider the equation $x^{2/3} + y^{2/3} = 4$. Find the equation of the tangent line at the point $(-3\sqrt{3}, 1)$.
  5. Given an equation in implicit form, should you manipulate the equation before applying the derivative to both sides?
  6. Here is the curve of $x^3 + y^3 = 6xy$:

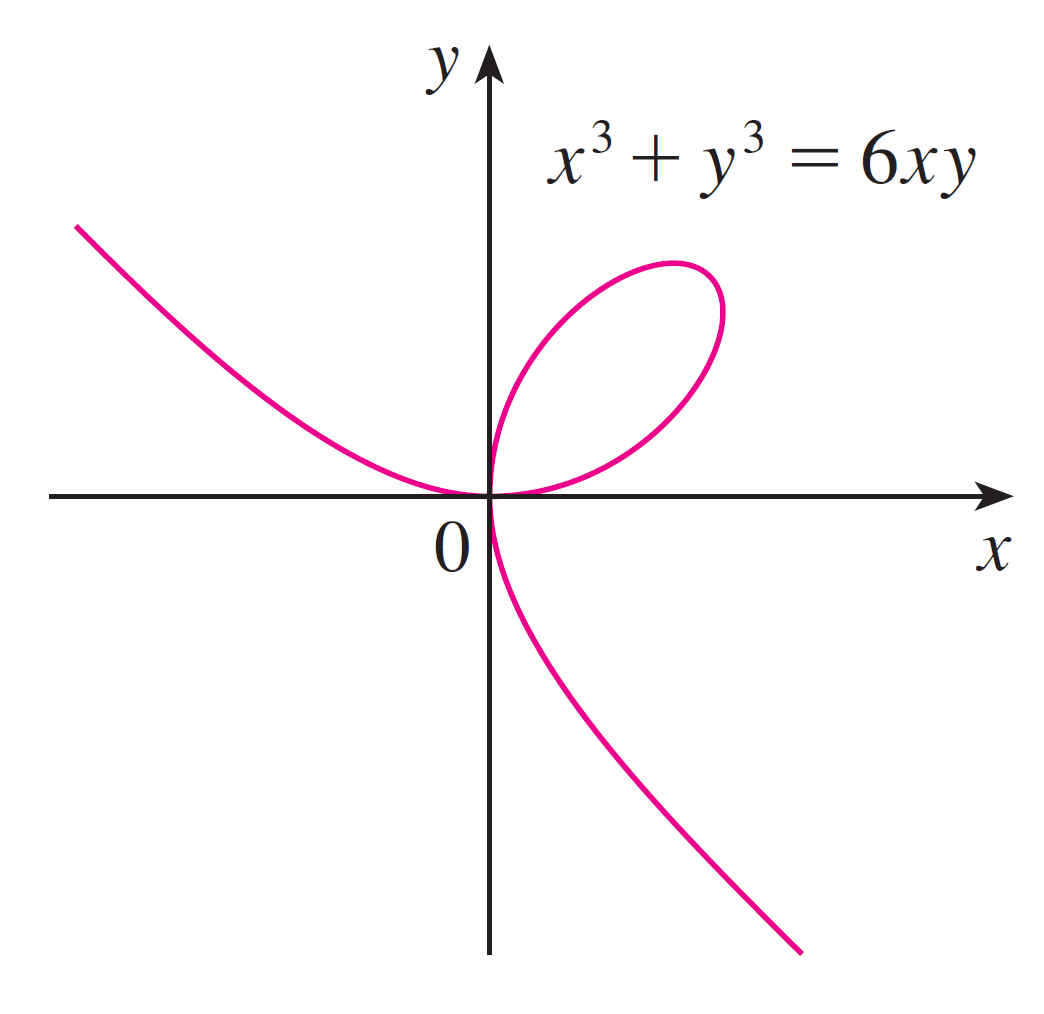
    In implicit differentiation, we assume $y = f(x)$ under suitable conditions. Draw multiple graphs which represent these "suitable conditions.".

    Hint: Chop up the curve so each part passes the vertical line test.

  7. Find $dy/dx$ with implicit differentiation:
    1. $x^2 - xy - y^2 = 4$
    2. $1 + x = \sin(xy)$
    3. $x^4y^3 + x^2y^4 = 2$
    4. $2\sqrt{x} + \sqrt{y} = 3$
    5. $(x + y)^3 + x^3 + y^3 = 0$
    6. $\dfrac{x}{y^3 - y} = 1$
    7. $\sin(x + y) = y^2 \cos x$
    8. $(x+y)^3 + x^3 + y^3 = 0$
    9. $e^{2y} + e^{2x} = 5$
  8. Find the equation of the tangent line at $(1,2)$ for the equation \[x^2 + 2xy - y^2 + x = 2\]
  9. Find the equation of the tangent line at $(\pi, \pi)$ for the equation \[\sin(x + y) = 2x - 2y\]
  10. Find the equation of the tangent line at $(-2,-2)$ for the equation \[x^3 + y^3 - \dfrac{17}{4}xy = 1\]
  11. The area of a triangle with lengths $a$ and $b$ and included angle $\theta$ is \[A = \frac{1}{2}ab \sin \theta\] If $a = 2$ cm, $b = 3$ cm, and $\theta$ is increasing at a rate of $0.2$ rad/min, how fast is the area increasing when $\theta = \frac{\pi}{3}$?
  12. The formula for the volume $V$ of a cube with side length $s$ is $V = s^3$. The sides of the cube are 5 feet long and increasing at the rate of $0.2$ inches/second. How fast is the volume of the cube changing?
  13. The kinetic energy of an object is $K = \frac{1}{2}mv^2$. If the object is accelerating at a rate of $9.8 \ m/s^2$, and the mass is $30$ kilograms, how fast is the kinetic energy increasing when the speed is $30$ meters per second?
    Hint: Kinetic energy is measured in units $\frac{kg \cdot m^2}{s^2}$, so the rate of change of kinetic energy must be in units $\dfrac{\frac{kg \cdot m^2}{s^2}}{s} = \frac{kg \cdot m^2}{s^3}$
  14. Suppose a drop of dye was dropped into a large bowl filled with water. If the dye spreads out in a circle and its radius is increasing at a rate of 2 cm/sec, determine how fast the area is increasing when the radius of the circle is 10 cm.
  15. A plane flying horizontally at an altitude of 1 mi and a speed of 500 mph passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 2 miles away from the station.

    16. The rest of these problems will appear on next week's homework. Skip the rest of these for this Homework.

  16. If the minute hand of a clock has length r (in centimeters) find the rate at which it sweeps out area as a function of r.
    Use the equation of a sector of a circle $A = \dfrac{1}{2}r^2 \theta$ (picture showing this below) and the fact that the rate at which the minute hand moves is $2\pi$ radians per hour.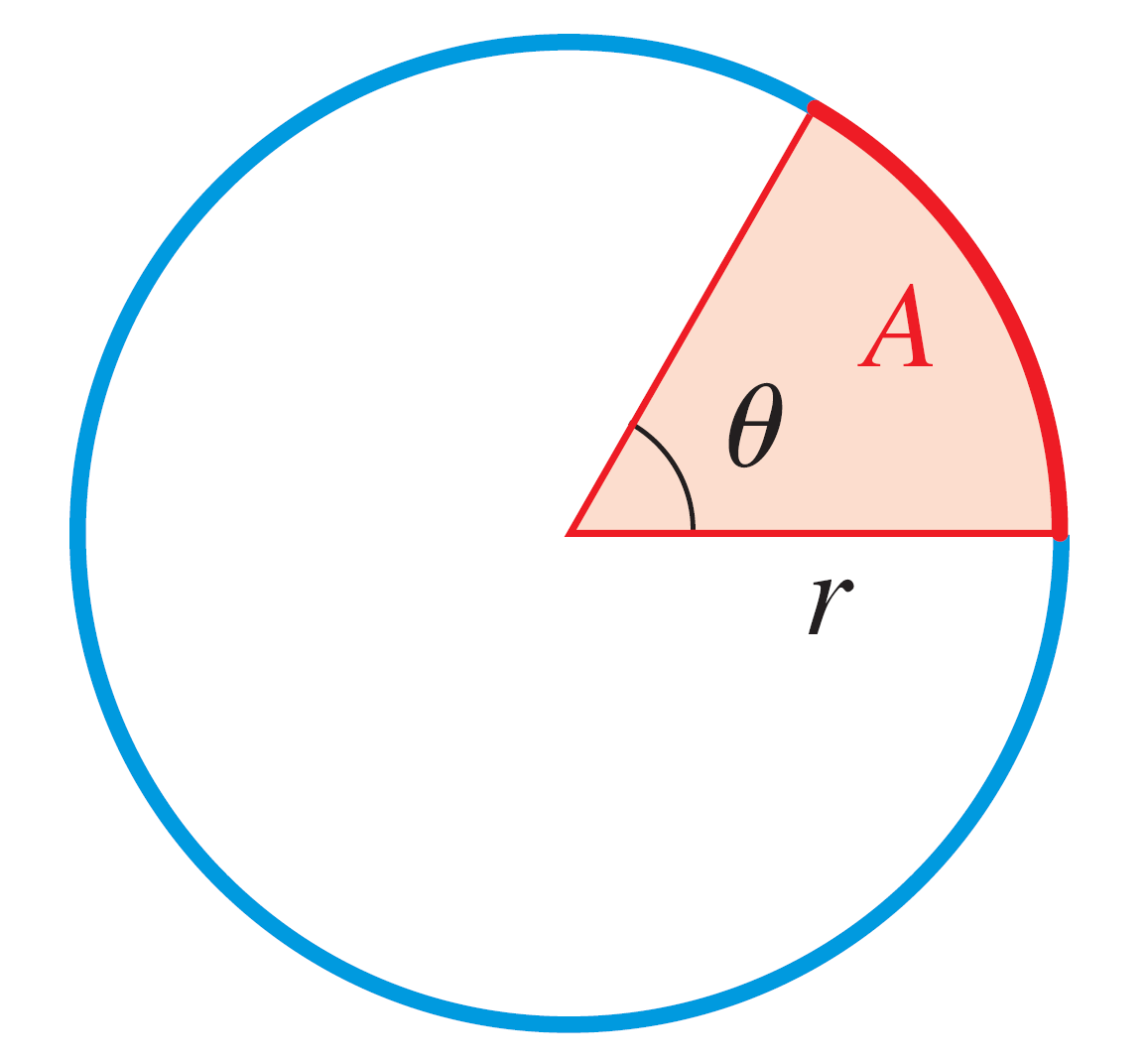
  17. Suppose a meat distributor is willing to make $x$ pounds of beef available every week on the marketplace when the price is $\$p$ per pound. The relationship between quantity supplied $x$ and price $p$ is \[650p^2 - x^2 = 100\] If 30,000 pounds of beef are available on the marketplace this week and the price per pound is falling by 2 cents per week, at what rate is the supply falling?

    Hint: the quantity supplied $x$ and the price per pound $p$ are quantities that change every week, or in other words, over time.

  18. Differentiate the following. Remember you can use logarithmic differentiation to simplify the form for some problems.
    1. $f(x) = x\ln x$
    2. $f(x) = \ln (\sin^2 x)$
    3. $f(x) = \sqrt[5]{\ln x}$
    4. $f(x) = \ln{\sqrt[5]{x}}$
    5. $y = \ln(e^{-x} + xe^{-x})$
    6. $y = \dfrac{\sin x \cos^2 x}{(x^2 + 1)^4}$
    7. $f(x) = x\ln x$
    8. $f(x) = x^{\cos x}$
    9. $f(x) = (\sin x)^{\sin x}$