2.3: Limits of Functions at Finite Numbers

In this section, instead of looking at \[\lim_{x\rightarrow\infty} f(x)\] we are interested in \[\lim_{x\rightarrow a} f(x)\]

Goals:

Define the limit of a function
Describe a tool for calculating the limit of a function.
Understand when a limit exists and what the graph looks like.
Describe pitfalls with this method.

The Table Method

There are usually three ways to find limits:

Make a table of values, see what $f(x)$ is approaching
Look at the graph
Limit laws

This section develops our skill with #1 and #2. Next section looks at #3.

Suppose $f(x)$ is defined when $x$ is near the number $a$. Then we write \[\lim_{x\rightarrow a} f(x) = L\] if we can make the values of $f(x)$ arbitrarily close to $L$ by taking $x$ sufficiently close to $a$ but never, ever $a$ itself.

I think about it like this: the heights $f(x)$ can be made as close to $L$ as possible when you move $x$ close to $a$ but never $a$ itself.

This results in three possible graphs: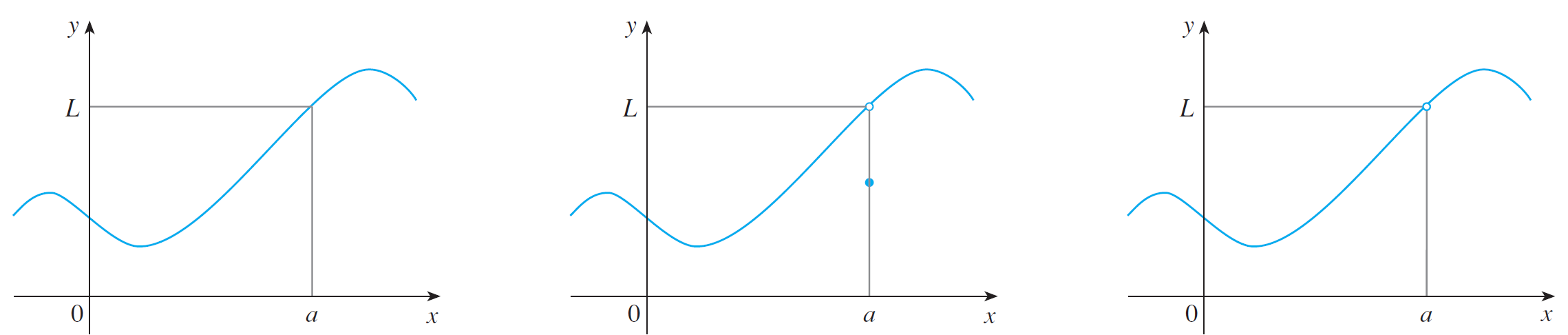

Our first tool for finding limits is called the table method.

Create two tables that samples $x$ values to the left and right of $a$ but never $a$. Do not plug in $a$!!!!

Then see what the values of $f(x)$ are approaching. If both tables agree then the limit exists.

Use the table method to guess the following limits:

$\displaystyle\lim_{x\rightarrow 1} \dfrac{x-1}{x^2 - 1}$
$\displaystyle\lim_{x\rightarrow 1} g(x)$ where \[g(x) = \begin{cases} \dfrac{x-1}{x^2 - 1} & x \neq 1 \\ 2 & x = 1 \end{cases}\]
$\displaystyle \lim_{x\rightarrow 0} \dfrac{\sin x}{x}$
$\displaystyle\lim_{x\rightarrow 0} \left(x^3 + \dfrac{\cos 5x}{10000}\right)$

These examples show that the table method has a big pitfall: potential inaccuracy if you don't pick $x$ close enough to $a$.

However, the left and the right table can be represented in limit notation.

One-Sided Limits

One-Sided Limits

The function $f$ has the right-hand limit $L$ as $x\rightarrow a$ from the right, written \[\lim_{x\rightarrow a^+} f(x) = L\] if $f(x)$ can be made close to $L$ as we please by taking $x$ sufficiently close to and to the right of $a$.

Similarly, the function $f$ has the left-hand limit $L$ as $x\rightarrow a$ from the left, written \[\lim_{x\rightarrow a^-} f(x) = L\] if $f(x)$ can be made close to $L$ as we please by taking $x$ sufficiently close to and to the left of $a$.

If left-and right-hand limits agree, the limit exists. This is equivalent to both tables agreeing. This idea is summarized as:

\[\lim_{x\rightarrow a^+}f(x) = L = \lim_{x\rightarrow a^-}f(x) \qquad \text{if and only if} \qquad \lim_{x\rightarrow a}f(x) = L\]

This theorem is very important. If left- and right-hand limits disagree, the limit does not exist.

For the Heaviside function \[H(t) = \begin{cases} 0 & t < 0 \\ 1 & t \geq 0\end{cases}\] determine if $\displaystyle\lim_{t\rightarrow 0}H(t)$ exists.

The Graph Method

Limits can also be seen on the graph: look at what the heights of the function are approaching on both sides of $x = a$.

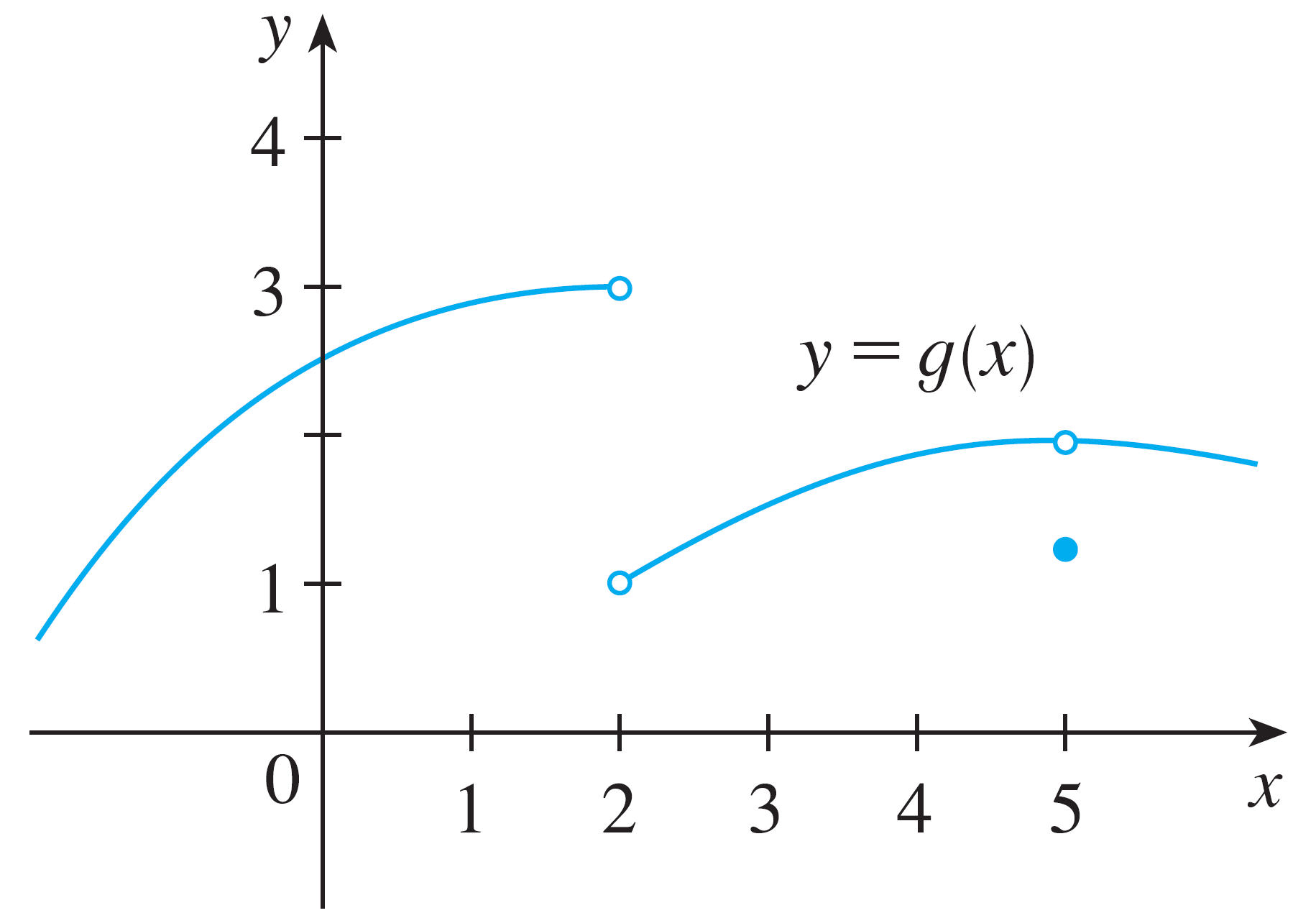A function $g(x)$ has the following graph:

Determine if the following exist. If they do, find the value.

$\displaystyle\lim_{x\rightarrow2^-} g(x)$
$\displaystyle\lim_{x\rightarrow2^+} g(x)$
$\displaystyle\lim_{x\rightarrow2} g(x)$
$\displaystyle\lim_{x\rightarrow5^-} g(x)$
$\displaystyle\lim_{x\rightarrow5^+} g(x)$
$\displaystyle\lim_{x\rightarrow5} g(x)$
$f(2)$
$f(5)$

Infinite Limits

Let $f$ be a function defined on both sides of $a$, except possibly at $a$. We write \[\lim_{x\rightarrow a} f(x) = \infty\] if $f(x)$ grows without bound by taking $x$ sufficiently close but not equal to $a$.

If $\lim_{x\rightarrow a}f(x) = -\infty$, then $f(x)$ is decreasing without bound.

These conditions are equivalent to the existence of a vertical asymptote.

The definition also applies to left- and right-hand limits.

Find \[\lim_{x\rightarrow 0} \dfrac{1}{x^2}\]

Find $\displaystyle\lim_{x\rightarrow 3^+} \dfrac{2x}{x-3}$ and $\displaystyle\lim_{x\rightarrow 3^-} \dfrac{2x}{x-3}$.