2.5: Continuity

Continuous Functions

In precalculus we learned that continuous functions are functions we can draw the graph of without lifting our pencil.

In calculus, use the previous sentence as intuition for the next definition:

A function $f$ is continuous at a number $x = a$ if the following conditions are satisfied:

$f(a)$ is defined.
$\displaystyle\lim_{x\rightarrow a}f(x)$ exists.
$\displaystyle\lim_{x\rightarrow a}f(x) = f(a)$.

If any of these conditions fail, then the function is not continuous.

Note: The limit $\lim_{x\rightarrow a}$ doesn't see what happens at $x = a$.

Continuity is the reason why the limit does equal to the value at $a$.

Given this graph of a function $f$:

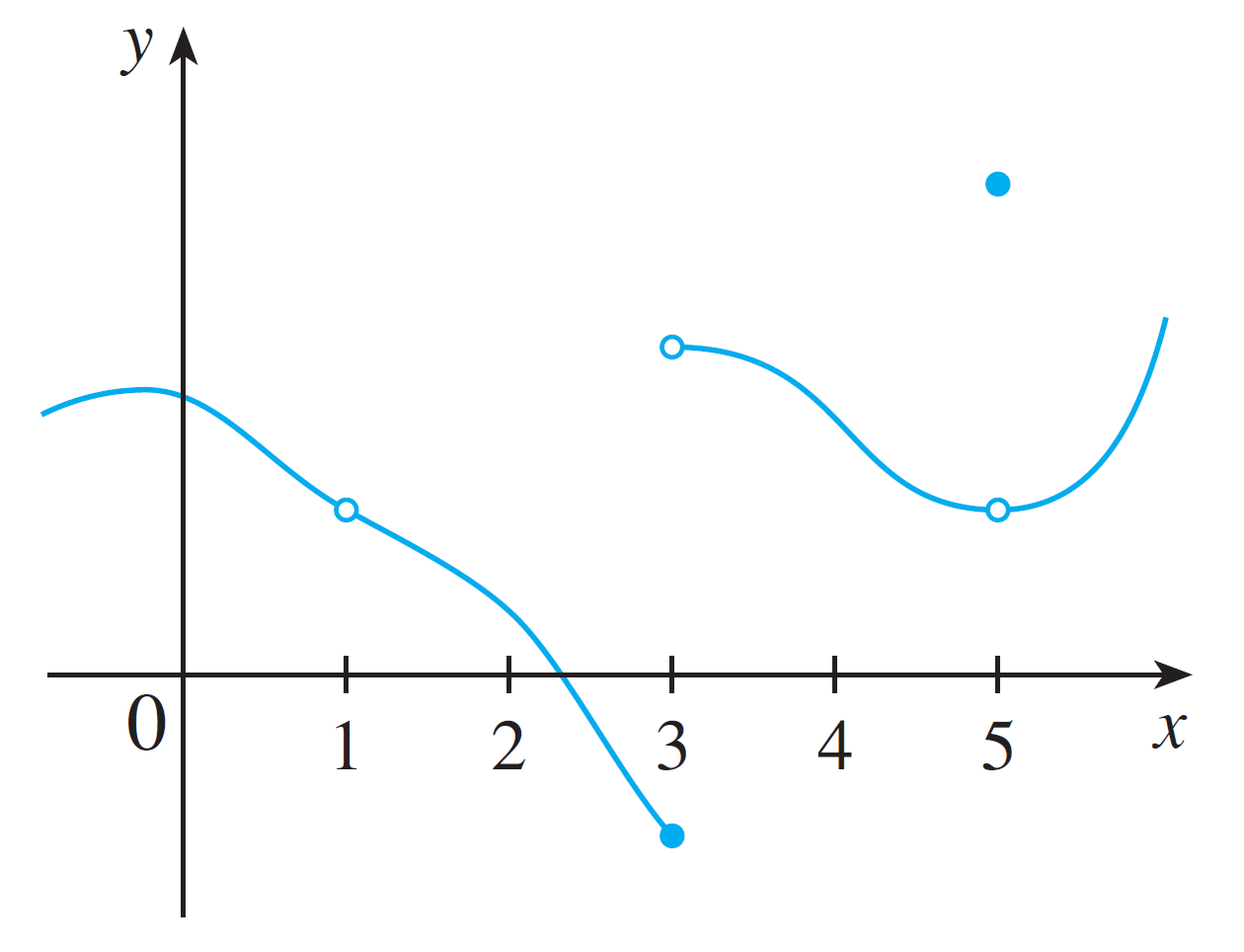
Where is the function not continuous and why?

In general:

A function $f$ is said to be continuous on an interval if $f$ is continuous on every number in the interval.
If $f$ is not continuous at $x = a$, it is said to be discontinuous at $x = a$.

To prove a function is continuous at $x = a$, you need to start with $\displaystyle \lim_{x\rightarrow a} f(x)$ and show that limit is equal to the evaluation $f(a)$.

Show $f(x) = x^3 + 3x^2$ is continuous at $x = 2$.

Use the definition of continuity to find out where each of the following functions are discontinuous:

$f(x) = \dfrac{x^2 - x - 2}{x-2}$
$f(x) = \begin{cases}\dfrac{1}{x^2} & x \neq 0 \\ 1 & x = 0\end{cases}$
$f(x) = \begin{cases}\dfrac{x^2-x-2}{x-2} & x \neq 2 \\ 1 & x = 2\end{cases}$
$f(t) = \begin{cases} 0 & t < 0 \\ 1 & t \geq 0 \end{cases}$

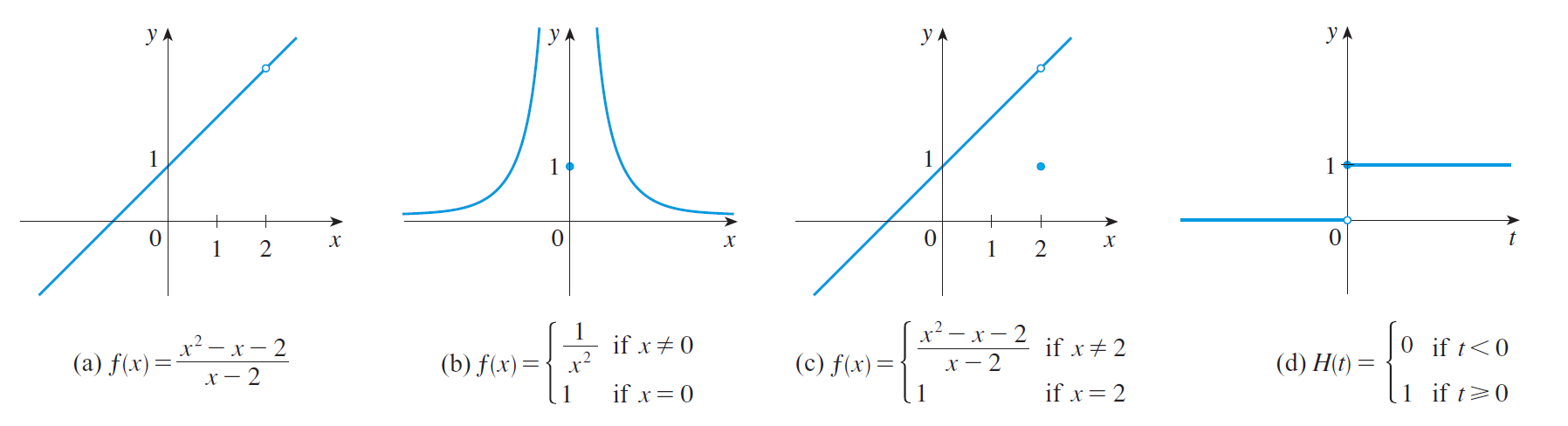
A few terminologies:

The discontinuity in (a) is called a removeable discontinuity because you can redefine $f(2)$ to make it continuous, hence removing the discontinuity.
The discontinuity in (b) is called an infinite discontinuity.
The discontinuity in (d) is called a jump discontinuity because the height $H(t)$ suddenly jumps from 0 to 1 when $t$ moves past 0.

Notice that $\displaystyle\lim_{t \rightarrow 0+} H(t) = H(0)$. We call this phenomena continuous from the right.

A function $f$ is continuous from the right at $x = a$ if \[\lim_{x\rightarrow a^+} f(x) = f(a)\] and continuous from the left if \[\lim_{x\rightarrow a^-} f(x) = f(a)\]

Which Functions are Continuous?

Finding where a function is continuous is really just a problem on finding the domain of that function. Let's see why:

A polynomial function of degree $n$ is a function of the form \[f(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_2x^2 + a_1x + a_0\qquad a_n \neq 0\] where $a_n, a_{n-1},\dots, a_1, a_0 \in \mathbb{R}$.

A rational function is a function of the form \[r(x) = \dfrac{p(x)}{q(x)}\] where $p(x)$ and $q(x)$ are both polynomials.

Examples of polynomials are \[x^5 + x^3 \qquad \qquad 4x^2 - x + 1 \qquad \qquad x^6 - 4x^4 - x^2\]

If $f$ and $g$ are continuous at $a$ and $c$ is a constant, then the following functions are also continuous at $a$:

$f + g$
$f - g$
$cf$
$fg$
$f/g$ if $g(a) \neq 0$

Suppose $f(x) = x^3$ and $g(x) = x^5$.

Limit Law 9 says for any $a \in \mathbb{R}$, we know \[\lim_{x\rightarrow a} f(x) = \lim_{x\rightarrow a } x^3 = a^3 = f(a) \qquad \qquad \lim_{x\rightarrow a}g(x) = \lim_{x\rightarrow a} x^5 = a^5 = g(a)\] We showed $f(x)$ and $g(x)$ are continuous on $\mathbb{R}$.

Using the previous fact: \[f(x) + g(x) = x^5 + x^3\] is continuous on $\mathbb{R}$.

This previous technique can be used to create any polynomial. Thus:

A polynomial function $P(x)$ is continuous on any value of $x$.
A rational function $R(x) = p(x)/q(x)$ is continuous on every value of $x$ where $q(x) \neq 0$.

This means if we take any limit of polynomial/rational, instead of limit laws, you can:

First find the domain of the function.
Then if $x = a$ is in the domain, just plug it in. Otherwise it might be an indeterminate form, does not exist, or $\pm\infty$ which we have seen how to deal with in Section 1.5 and 1.6.

Find \[\lim_{x\rightarrow -2} \dfrac{x^3 + 2x^2 - 1}{5 - 3x}\]

Turns out most of the functions we know about are continuous.

The following functions are continuous at every number in their domains:

polynomials
root functions
exponential functions
rational functions
trigonometric functions
logarithmic functions

Find \[\lim_{x\rightarrow\pi}\dfrac{\sin x}{2 + \cos x}\]

The previous theorem makes finding where a function is continuous into a domain problem.

Where is $h(x) = \sqrt{x} + \dfrac{x+1}{x-1} - \dfrac{x + 1}{x^2 + 1}$ continuous?

How about compositions?

Where are the following functions continuous?

$h(x) = \sin (x^2)$
$F(x) = \dfrac{1}{\sqrt{x^2 + 7} - 4}$

We found where these composed functions are continuous by finding the domain.

Here's why this works. The composition of continuous functions result in a continuous function:

If $f$ is continuous at $b$ and $\displaystyle\lim_{x\rightarrow a}g(x) = b$, then $\displaystyle\lim_{x\rightarrow a}f(g(x)) = f(b)$. In other words: \[\lim_{x\rightarrow a} f(g(x)) = f\left(\lim_{x\rightarrow a} g(x)\right)\]

Think of this as the limit symbol can swap places with the function symbol, only if the function is continuous.

Use the previous theorem to evaluate the following limit: \[\lim_{x\rightarrow\sqrt{\pi}} \sin(x^2)\]

Intermediate Value Theorem

Here is one application of continuity.

You are driving to Lake Tahoe from San Luis Obispo.

The distance traveled after $t$ seconds is determined by the function \[f(t) = 4t^2 , \ t \geq 0\] where $f(t)$ is in feet.

At time $t = 0$, you are at position $f(0) = 0$; you hasn't moved from your starting position.

At time $t = 10$, you are at position $f(10) = 400$. This means you are 400 feet away from your starting position after 10 seconds.

This function is continuous on $[0, \infty)$. Intuitively, this means your car cannot suddenly teleport from one location to another.

As such, if we were to ask "is there a time $t$ where $f(t) = 100$?", the answer must be yes.

This is called the Intermediate Value Theorem.

Intermediate Value Theorem
Suppose $f$ is continuous on $[a, b]$ and let $N$ be any number between $f(a)$ and $f(b)$ where $f(a) \neq f(b)$. Then there exists $c$ in $(a, b)$ such that $f(c) = N$.

Existence of Zeros of a Continuous Function
If $f$ is a continuous function on a closed interval $[a,b]$ and $f(a)$ and $f(b)$ have opposite signs, then there exists $c \in (a, b)$ where $f(c) = 0$.

Let $f(x) = 4x^3 - 6x^2 + 3x - 2$.

Show $f$ is continuous for all $x \in \mathbb{R}$.
Show there exists at least one $c \in (1,2)$ where $f(c) = 0$.