3.1: Derivatives and Rates of Change

We will study a special type of limit called a derivative. These arise when we are looking at an instantaneous rate of change, the slope of a tangent line, or a velocity.

Tangents

This lecture note describes the intuition behind creating a tangent line.

We saw it was a limit. Here's the definition:

The tangent line to the curve $y = f(x)$ at the point $P(a, f(a))$ is the line through $P$ with slope \[m = \lim_{x\rightarrow a}\dfrac{f(x) - f(a)}{x - a}\] if this limit exists.
Find an equation of the tangent line to the parabola $y = x^2$ at the point $P(1,1)$.

The tangent line limit is an indeterminate form. Here is an animation of the previous example:

Notice how the expression $f(x) - f(a)$ approaches $0$ and $x - a$ also approaches 0.

Because this limit is an indeterminate form, we need to simplify the expression before applying the limit.

In practice, it's easier to simplify the following equivalent expression of the slope of the tangent line: \[m = \lim_{h \rightarrow 0} \dfrac{f(a + h) - f(a)}{h}\]

Find an equation of the tangent line to the hyperbola $y = 3/x$ at the point $(3, 1)$.

The tangent line is sometimes called the slope of the curve because if you zoom in far enough, the curve almost looks like a straight line.

Instantaneous Rates of Change

If $f(x)$ is a function, we can analyze "on average" how much $f(x)$ changes over an interval $[a, a + h]$.

For example, a position function $s = f(t)$ gives the total distance traveled of an object moving in a straight line $t$ seconds after rest.

Suppose you are traveling from San Luis Obispo to Lake Tahoe. The total distance traveled from your home is modeled by \[f(t) = 60t^2 \qquad 0 \leq 0 \leq t \leq 6\] where $t$ is in hours and $f(t)$ is in miles.
  1. How far have you travelled after one hour and two hours?
  2. How far did you travel between one hour and two hours?

Over the time interval $[a, a+h]$, the change in position is $f(a + h) - f(a)$. Thus the average velocity is \[\text{average velocity} = \dfrac{\text{total displacement}}{\text{total time elapsed}} = \dfrac{f(a + h) - f(a)}{h}\]

We want the instantaneous rate of change at $x = a$, or how fast the function is changing exactly at one $x$-value.

In the context of velocity, we can look at shorter and shorter time periods of the average velocity. This requires $h \rightarrow 0$. Thus we have the following definition:

The instantaneous velocity $v(a)$ at time $t = a$ is the limit of the average velocities \[v(a) = \lim_{h \rightarrow 0} \dfrac{f(a + h) - f(a)}{h}\]

Think of instantaneous velocity as reading off your speedometer in the car at one point in time!

Suppose that a ball is dropped from the upper observation deck of the CN Tower in Toronto, 450 m above the ground. Find the instantaneous velocity of the ball after 5 seconds.

Derivatives

Notice how the same limit \[\lim_{h\rightarrow 0} \dfrac{f(a + h) - f(a)}{h}\] occurred when we wanted to calculate a "rate of change" or a tangent line. This limit appears often enough so we give it a name:

The derivative of a function $f$ at a number $a$, denoted by $f'(a)$ is \[f'(a) = \lim_{h\rightarrow 0} \dfrac{f(a+h) - f(a)}{h}\] if this limit exists.

The derivative can take on three interpretations:

  1. It is the slope of the tangent line at $x = a$.
  2. It is the "instantaneous rate of change" at $x = a$. For example:
    • If $s(t)$ is a position function, then $s'(a)$ is the instantaneous velocity at the moment in time $t = a$.
    • Think of this interpretation as how fast the heights $f(x)$ are changing at the $x$-value $a$.
  3. It is the slope of the curve at $x = a$. In particular, you should think of the tangent line as an "approximation" to the function $f(x)$.

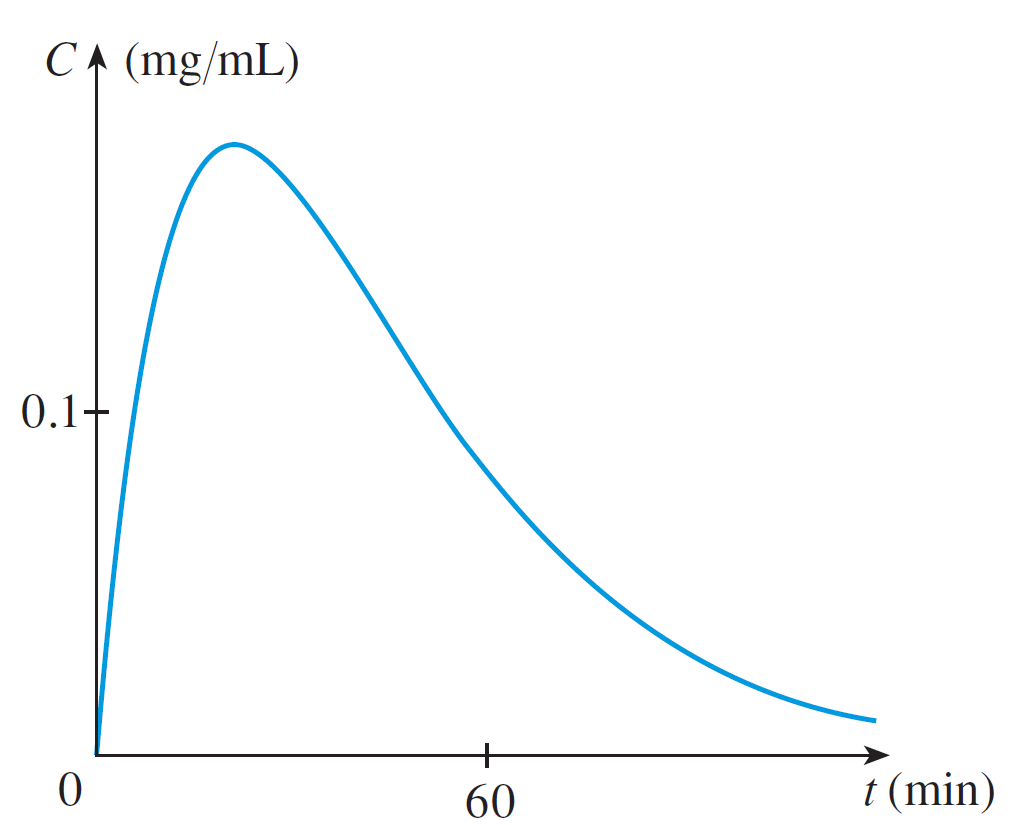
Find the derivative of the function $f(x) = x^2 - 8x + 9$ at the number $a$.
Medical researchers measured the blood alcohol concentration (BAC) of eight fasting adult male subjects after rapid consumption of 15 mL of ethanol (corresponding the one alcoholic drink). The data they obtained were modeled by the concentration function \[f(x) = 0.0225xe^{-0.0467x}\] where $x$ is in minutes after consumption and $f(x)$ is measured in mg/mL.

How quickly is the BAC increasing after 10 minutes?

Solution: You are asked to find the instantaneous rate of change of $f(x)$ at $x = 10$.

This is equivalent to finding the slope of the tangent line at $x = 10$.

The slope of the tangent line is the derivative.

Thus the tangent line to $y = f(x)$ at $(a, f(a))$ is the line through $(a, f(a))$ whose slope is $f'(a)$.

The general equation can be described with point-slope form.

Suppose $f(x)$ is a function. The equation of the tangent line at the point $(a, f(a))$ is \[y - f(a) = f'(a) (x - a)\]
Find an equation of the tangent line to the parabola $y = x^2 - 8x + 9$ at the point $(3, -6)$.