4.1: Maximum and Minimum Values
Absolute and Local Extreme Values
Let $c$ be in the domain $D$ of $f(x)$. Then $f(c)$ is the
- absolute maximum value of $f$ if $f(c) \geq f(x)$ for all $x \in D$ and
- absolute minimum value of $f$ if $f(c) \leq f(x)$ for all $x \in D$.
The comparison above was with all numbers in the domain. We can restrict our context to just be near a point instead.
The number $f(c)$ is a
- local maximum value of $f$ if $f(c) \geq f(x)$ when $x$ is near $c$ and
- local minimum value of $f$ if $f(c) \leq f(x)$ when $x$ is near $c$.
Identify all absolute/local minimums and maximums for the following function:

Identify all absolute/local minimums and maximums for $f(x) = x^2$ and $f(x) = x^3$.
When do absolute extrema exist? Turns out you only need two requirements.
The Extreme Value Theorem
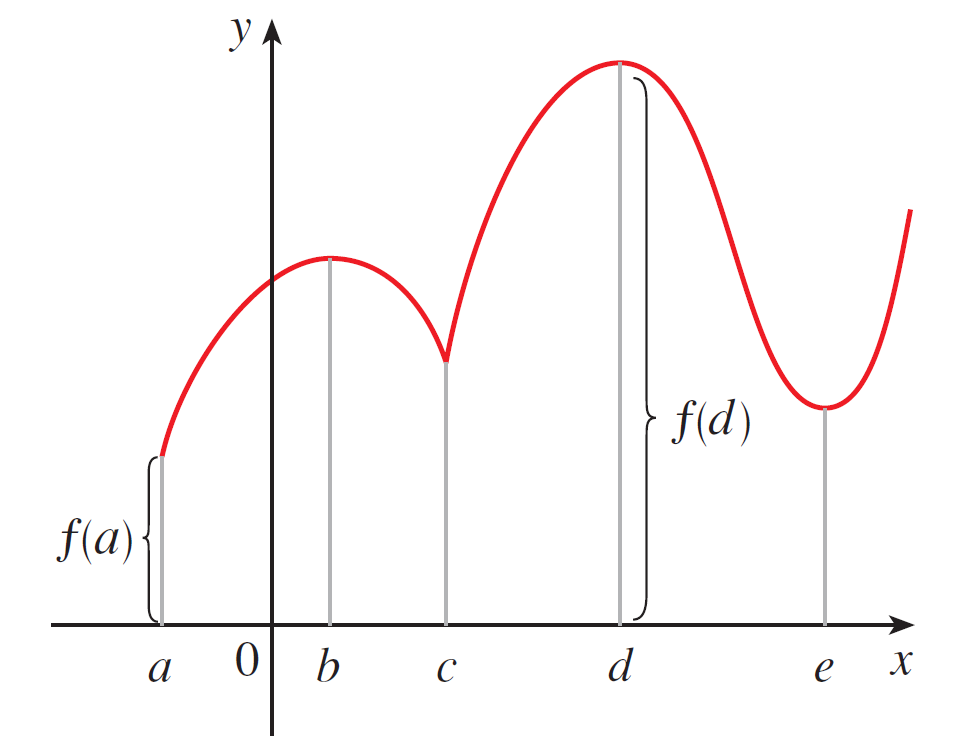
If $f$ is continuous on a closed interval $[a, b]$, then $f$ is guaranteed to have an absolute maximum $f(c)$ and an absolute minimum $f(d)$ for some $c,d \in [a, b]$.
If $f$ is continuous on a closed interval $[a, b]$, then $f$ is guaranteed to have an absolute maximum $f(c)$ and an absolute minimum $f(d)$ for some $c,d \in [a, b]$.
*pictures in class*
The Closed Interval Method
We are interested in locating where the absolute minimum/maximum occur.
These graphs show absolute min/max can occur at a local min/max or an endpoint.
If it is at a local min/max, then either $f'(c) = 0$ or there is a corner at $c$, meaning $f'(c)$ does not exist. Such numbers are given a name:
A critical number of $f$ is a number $c$ where $f'(c) = 0$ or $f'(c)$ does not exist.
Find all critical numbers of $f(x) = x^{3/5}(4 - x)$.
Find all critical numbers $f(x) = x^3 + 3x^2 - 24x$.
The Closed Interval Method
To find the absolute maximum and minimum values of a continuous function $f$ on a closed interval $[a, b]$:
To find the absolute maximum and minimum values of a continuous function $f$ on a closed interval $[a, b]$:
- Find the values of $f$ at the critical numbers of $f$ in $(a, b)$.
- Find the values of $f$ at the endpoints of the interval.
- The largest number from Steps 1 and 2 is the absolute maximum and the smallest is the absolute minimum.
Find the absolute extrema of the function \[f(x) = x^3 - 2x^2 - 4x + 4\] on $[0, 3]$.
Find the absolute extrema of \[f(x) = x^{2/3}\] on $[-1, 8]$.