Homework 9
Directions:
- Show each step of your work and fully simplify each expression.
- Turn in your answers in class on a physical piece of paper.
- Staple multiple sheets together.
- Feel free to use Desmos for graphing.
Answer the following:
- Draw a function with a domain of $[-10, 10]$, concave upward on $[-10, -2]$, concave downward on $[-2, 5]$, concave up on $[5, 10]$ and $f'(5)$ does not exist.
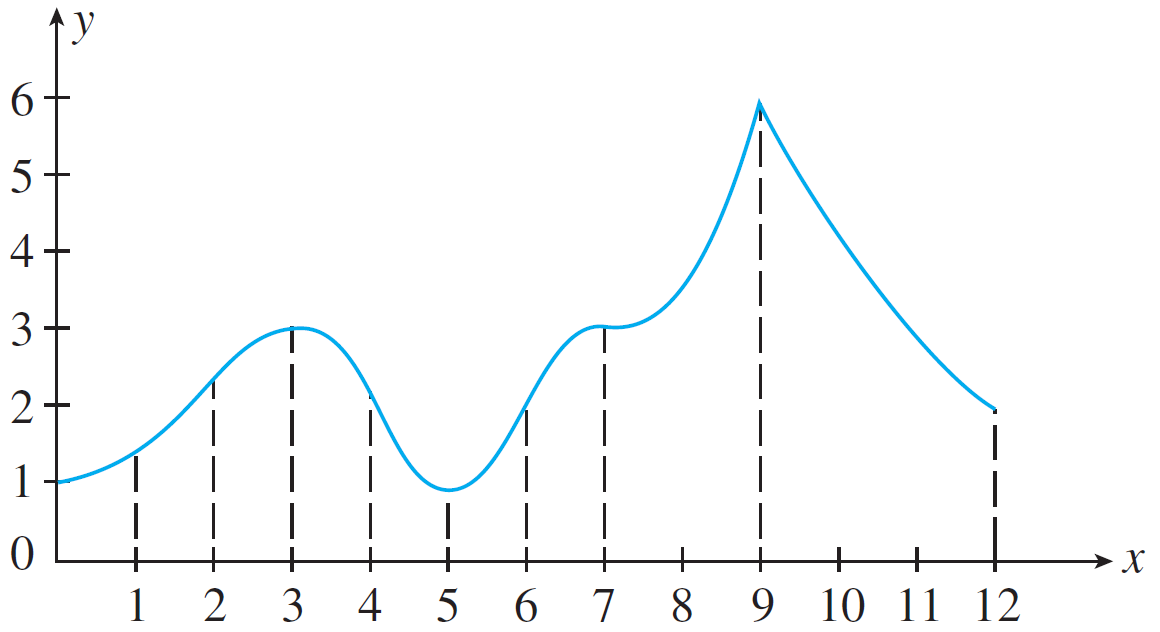
- For the following function
Determine the intervals of concavity and all of the inflection points.
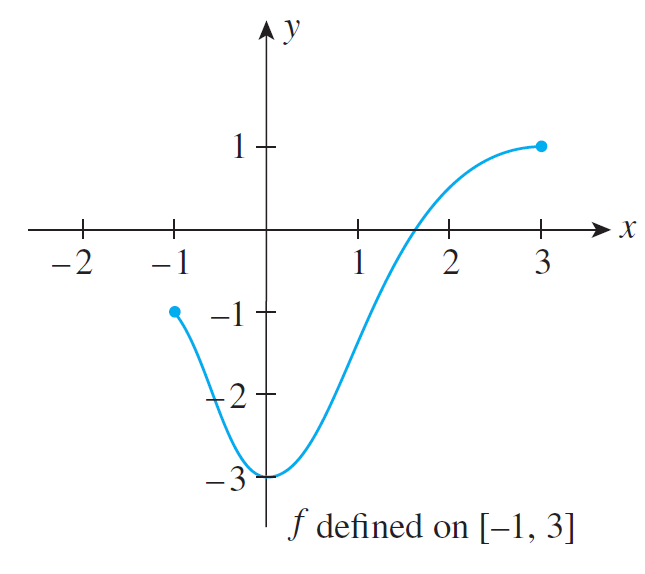
- For the following function
- Find the intervals of concavity.
- Determine all of the inflection points.
- Explain why the second derivative is conclusive of a relative extrema at $x=3$ and at $x = 5$.
- Explain why the second derivative fails to determine if there is a relative extrema at $x = 7$ and $x = 9$.
- Draw a graph with $f'(0)$ undefined, $f$ is decreasing on $(-\infty, 0)$, $f$ is concave down on $(0, 3)$, and $f$ has an inflection point at $x = 3$.
-
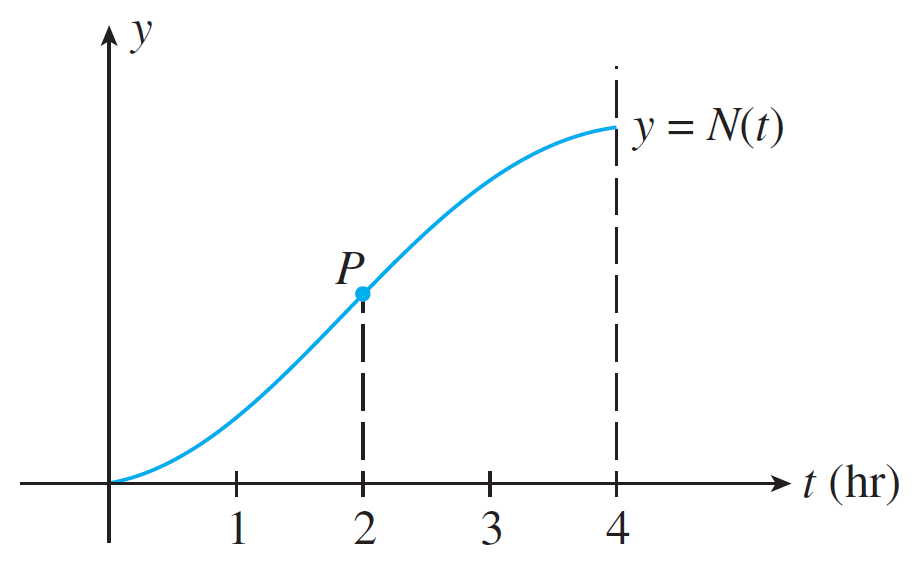
Suppose the following function $N(t)$ gives the total number of customers served at a McDonalds every hour where $t = 0$ is 8 AM.
- What is the rate of change of the total number of customers served? Why does this make sense in context?
- Determine the intervals of concavity.
- For each interval above, interpret in English the meaning of concavity in context.
-
Determine where each of the following functions are concave upward and concave downward.
- $f(x) = 2x^2 - 3x + 4$
- $f(x) = \dfrac{1}{x - 2}$
- $f(x) = \dfrac{x}{1 + x^2}$
- $f(x) = x + \dfrac{1}{x^2}$
-
$f(x) = \dfrac{x}{1+x^2}$
Hint: your second derivative will simplify to $\dfrac{2x(x^2 - 3)}{(x^2 + 1)^3}$
- Find the inflection points of $g(x) = x^3 - 6x$.
-
Use the second derivative test to find the relative extrema of the following functions:
- $f(x) = x + \dfrac{9}{x}$
- $f(x) = 2x^3 + 3x^2 - 12x - 4$
- The altitude (in meters) of a rocket $t$ seconds into flight is given by the function \[f(t) = -t^3 + 54t^2 + 480t + 6 \qquad t \geq 0\] What is the maximum upwards velocity (not maximum altitude) attained by the rocket?
-
Find the absolute maximum and minimum values (if any) of the following functions:
- $f(x) = \dfrac{1}{x}$ on $(0, \infty)$
- $f(x) = \dfrac{x + 1}{x-1}$ on $[2, 4]$
- $f(x) = x^2 - 2x - 3$ on $[-2, 3]$
- Mustang village has 100 two-bedroom units. The monthly profit (in dollars) realized from renting out $x$ apartments is given by \[P(x) = -10x^2 + 1760x - 50000\] To maximize the monthly rental profit, how many units should be rented out? (Hint: This is an absolute extrema problem. We can use the Closed Interval Test).
- Find the absolute extrema of the following function: