Homework 9

Directions:

1. Show each step of your work and fully simplify each expression.
2. Turn in your answers in class on a physical piece of paper.
3. Staple multiple sheets together.
4. Feel free to use Desmos for graphing.

Answer the following:

1. Draw a function with a domain of $[-10, 10]$, concave upward on $[-10, -2]$, concave downward on $[-2, 5]$, concave up on $[5, 10]$ and $f'(5)$ does not exist.
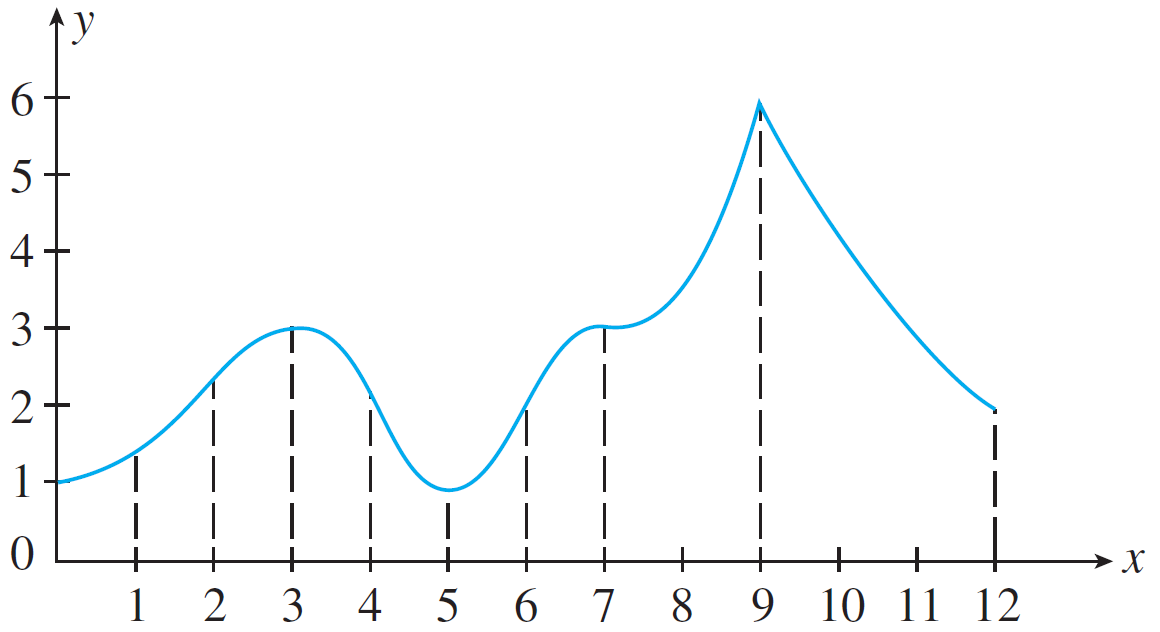
2. For the following function Determine the intervals of concavity and all of the inflection points.
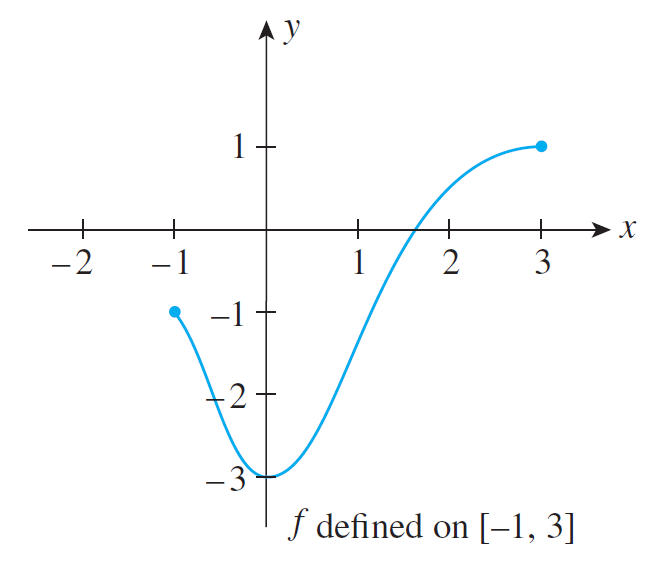
3. For the following function
   1. Find the intervals of concavity.
   2. Determine all of the inflection points.
   3. Explain why the second derivative is conclusive of a relative extrema at $x=3$ and at $x = 5$.
   4. Explain why the second derivative fails to determine if there is a relative extrema at $x = 7$ and $x = 9$.
4. Draw a graph with $f'(0)$ undefined, $f$ is decreasing on $(-\infty, 0)$, $f$ is concave down on $(0, 3)$, and $f$ has an inflection point at $x = 3$.
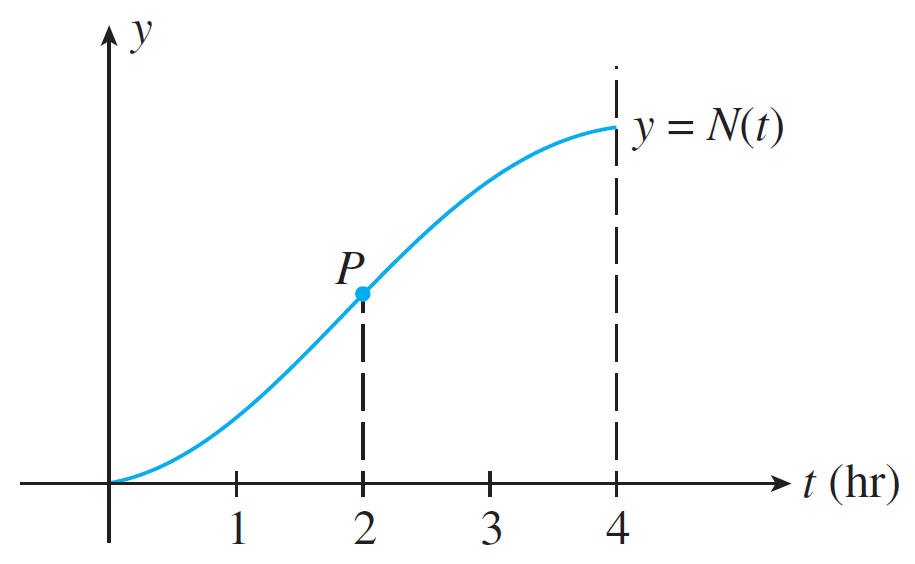
5. Suppose the following function $N(t)$ gives the total number of customers served at a McDonalds every hour where $t = 0$ is 8 AM.
   1. What is the rate of change of the total number of customers served? Why does this make sense in context?
   2. Determine the intervals of concavity.
   3. For each interval above, interpret in English the meaning of concavity in context.
6. Determine where each of the following functions are concave upward and concave downward.
   1. $f(x) = 2x^2 - 3x + 4$
   2. $f(x) = \dfrac{1}{x - 2}$
   3. $f(x) = \dfrac{x}{1 + x^2}$
   4. $f(x) = x + \dfrac{1}{x^2}$
   5. $f(x) = \dfrac{x}{1+x^2}$
      Hint: your second derivative will simplify to $\dfrac{2x(x^2 - 3)}{(x^2 + 1)^3}$
7. Find the inflection points of $g(x) = x^3 - 6x$.
8. Use the second derivative test to find the relative extrema of the following functions:
   1. $f(x) = x + \dfrac{9}{x}$
   2. $f(x) = 2x^3 + 3x^2 - 12x - 4$
9. The altitude (in meters) of a rocket $t$ seconds into flight is given by the function \[f(t) = -t^3 + 54t^2 + 480t + 6 \qquad t \geq 0\] What is the maximum upwards velocity (not maximum altitude) attained by the rocket?
10. Find the absolute maximum and minimum values (if any) of the following functions:
    1. $f(x) = \dfrac{1}{x}$ on $(0, \infty)$
    2. $f(x) = \dfrac{x + 1}{x-1}$ on $[2, 4]$
    3. $f(x) = x^2 - 2x - 3$ on $[-2, 3]$
11. Mustang village has 100 two-bedroom units. The monthly profit (in dollars) realized from renting out $x$ apartments is given by \[P(x) = -10x^2 + 1760x - 50000\] To maximize the monthly rental profit, how many units should be rented out? (Hint: This is an absolute extrema problem. We can use the Closed Interval Test).
12. Find the absolute extrema of the following function: