2.5: One-Sided Limits and Continuity

One-Sided Limits

We saw the use of approaching from the left and right to determine if a limit exists. Let's make the notation rigorous under the limit laws.

One-Sided Limits

The function $f$ has the right-hand limit $L$ as $x\rightarrow a$ from the right, written \[\lim_{x\rightarrow a^+} f(x) = L\] if $f(x)$ can be made close to $L$ as we please by taking $x$ sufficiently close to and to the right of $a$.

Similarly, the function $f$ has the left-hand limit $L$ as $x\rightarrow a$ from the left, written \[\lim_{x\rightarrow a^-} f(x) = L\] if $f(x)$ can be made close to $L$ as we please by taking $x$ sufficiently close to and to the left of $a$.

Note that the limit laws hold for left and right hand limits as well.

If left and right hand limits agree, the limit exists:

Let $f(x)$ be a function and $a,b\in \mathbb{R}$ where $b$ is close to $a$. Suppose $f(b)$ is defined, but possibly $f(a)$ is not. Then \[\lim_{x\rightarrow a^+}f(x) = L = \lim_{x\rightarrow a^-}f(x) \qquad \text{if and only if} \qquad \lim_{x\rightarrow a}f(x) = L\]
Let \[f(x) = \begin{cases} -x & x \leq 0 \\ \sqrt{x} & x > 0 \end{cases}\qquad g(x) = \begin{cases} -1 & x < 0 \\ 1 & x \geq 0 \end{cases}\]
  1. Show $\lim_{x\rightarrow 0} f(x)$ exists and find the value by using one-sided limits.
  2. Show $\lim_{x\rightarrow 0} g(x)$ does not exist.

Continuous Functions

In precalculus we learned that continuous functions are functions we can draw the graph of without lifting our pencil.

In calculus, use the previous sentence as intuition for the next definition:

A function $f$ is continuous at a number $x = a$ if the following conditions are satisfied:
  1. $f(a)$ is defined.
  2. $\displaystyle\lim_{x\rightarrow a}f(x)$ exists.
  3. $\displaystyle\lim_{x\rightarrow a}f(x) = f(a)$.

If any of these conditions fail, then the function is not continuous.

Given this graph of a function $f$:

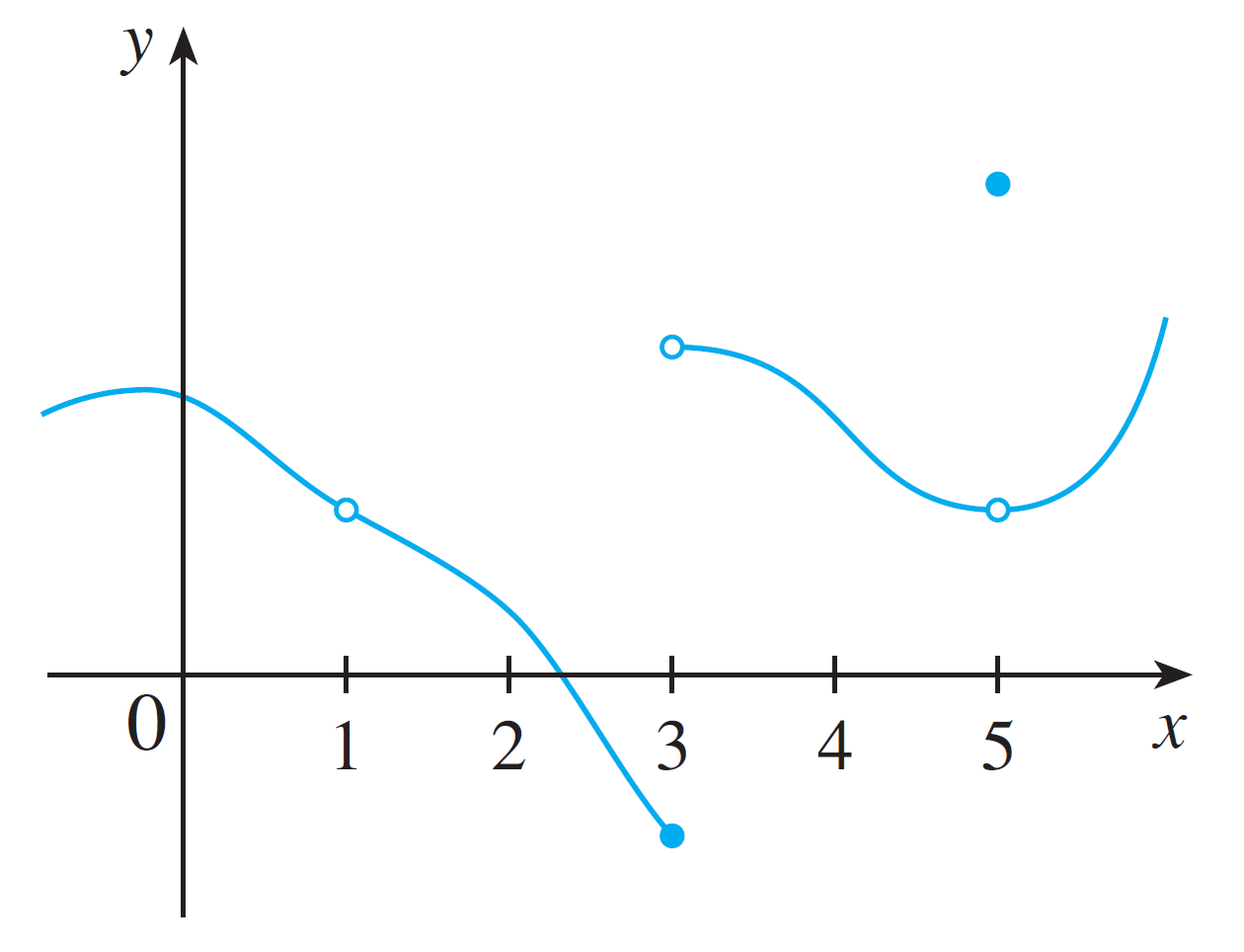
Where is the function not continuous?

In general:
  1. A function $f$ is said to be continuous on an interval if $f$ is continuous on every number in the interval.
  2. If $f$ is not continuous at $x = a$, it is said to be discontinuous at $x = a$.
Find the values of $x$ where each function is continuous:
  1. $f(x) = x + 2$
  2. $g(x) = \dfrac{x^2-4}{x-2}$
  3. $h(x) = \begin{cases} \frac{1}{x} & x > 0 \\ -1 & x \leq 0\end{cases}$

Properties of Continuous Functions

  1. If $c \in \mathbb{R}$, then $f(x) = c$ is continuous everywhere.
  2. $f(x) = x$ is continuous everywhere.
Now if $f$ and $g$ are continuous at $x = a$, then
  1. $[f(x)]^n$ is continuous at $x = a$ if it is defined.
  2. $f\pm g, f\cdot g$ is continuous at $x = a$.
  3. $f/g$ is continuous at $x = a$ if $g(a) \neq 0$.
If you take facts 2,3,4, we can create polynomial functions. Including fact 5 gives us rational functions. So in general:
  1. A polynomial function $P(x)$ is continuous on any value of $x$.
  2. A rational function $R(x) = p(x)/q(x)$ is continuous on every value of $x$ where $q(x) \neq 0$.
This means if we take any limit (except for limit at infinity) for polynomial and rational functions, we can just plug in the value!
Find the values of $x$ where each function is continuous:
  1. $f(x) = 3x^3 + 2x^2 - x + 10$
  2. $f(x) = \dfrac{8x^{10} - 4x + 1}{x^2 + 1}$
  3. $f(x) = \dfrac{4x^3 - 3x^2 + 1}{x^2 - 3x +2}$

Intermediate Value Theorem

Suppose a maglev's position at time $t$ is determined by the function \[f(t) = 4t^2 \qquad 0 \leq t \leq 10\]

Consider the endpoints. At time $t = 0$, the maglev is at position $f(0) = 0$; it hasn't moved from its starting position.

At time $t = 10$, the maglev is at position $f(10) = 400$. This means the maglev is 400 units away from it's starting position.

This function is continuous. Intuitively, this means the maglev cannot "suddenly" jump over portions of the track; it must always be on the track.

As such, if we were to ask "is there a time $t$ where $f(t) = 100$?", the answer must be yes. This is called the Intermediate Value Theorem.

Intermediate Value Theorem
If $f$ is a continuous function on a closed interval $[a, b]$ and $M$ is any number between $f(a)$ and $f(b)$, then there is at least one number $c$ in $[a,b]$ such that $f(c) = M$.
Existence of Zeros of a Continuous Function
If $f$ is a continuous function on a closed interval $[a,b]$ and $f(a)$ and $f(b)$ have opposite signs, then there exists $c \in (a, b)$ where $f(c) = 0$.
Let $f(x) = x^3 + x + 1$.
  1. Show $f$ is continuous for all $x \in \mathbb{R}$.
  2. Show there exists at least one $c \in (-1, 1)$ where $f(c) = 0$.