Homework 7

Directions:

  1. Show each step of your work and fully simplify each expression.
  2. Turn in your answers in class on a physical piece of paper.
  3. Staple multiple sheets together.
  4. Feel free to use Desmos for graphing.

Answer the following:

  1. For each of the following functions, do the following:
    • Find the values of all local minima and maxima.
    • Find the intervals where $f(x)$ is increasing and decreasing.
    1. $f(x) = x^3 - 3x^2 - 9x + 4$
    2. $f(x) = 2x^3 - 9x^2 + 12x - 3$
    3. $f(x) = x\sqrt{6-x}$
    4. $f(x) = \dfrac{x}{x^2 + 1}$
    5. $f(x) = (x+1)^5 - 5x - 2$
    6. $f(x) = x - \sin x$ on the interval $0 \leq x \leq 4\pi$.
  2. For each of the previous functions, find all the inflection points and the intervals of concavity.
  3. Sketch a graph of a function which satisfies the following conditions:
    • $f'(0) = f'(2) = f'(4) = 0$
    • $f'(x) > 0$ when $x < 0$ or $2 < x < 4$
    • $f'(x) < 0$ when $0 < x < 2$ or $x > 4$
  4. Sketch a graph of a function which satisfies the following conditions:
    • vertical asymptote $x = 0$
    • $f'(x) > 0$ when $x < -2$
    • $f'(x) < 0$ when $x > -2$ and $x \neq 0$
    • $f''(x) < 0$ when $x < 0$
    • $f''(x) > 0$ when $x > 0$
  5. Sketch a graph of a function which satisfies the following conditions:
    • $f'(5) = 0$
    • $f'(x) < 0$ when $x < 5$
    • $f(x) > 0$ when $x > 5$
    • $f''(2) = 0$ and $f''(8) = 0$
    • $f''(x) < 0$ when $x < 2$ or $x > 8$
    • $f''(x) > 0$ when $2 < x < 8$
  6. A function $f(x)$ has the graph of its derivative $f'(x)$ shown below: 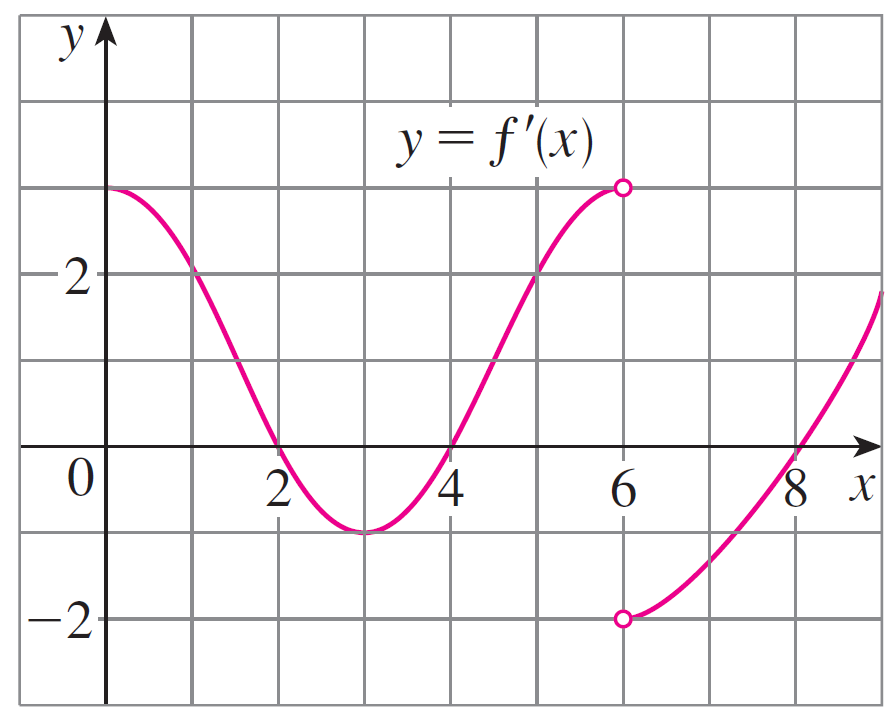Answer the following:
    1. On what intervals is $f(x)$ increasing and decreasing?
    2. At what values of $x$ does $f(x)$ have a local maximum and minimum?
    3. What intervals are $f(x)$ concave upward and downward?
    4. State the $x$-coordinates of the point(s) of inflection.
  7. Use the Second Derivative Test to find the local maximums and minimums for the following functions:
    1. $f(x) = \dfrac{1}{2} x^4 - 4x^2 + 3$
    2. $f(x) = 5x^3 - 3x^5$
  8. In Section 3.1 we saw the function $f(x) = x^{2/3}$ had a local minimum in the shape of a corner at $x = 0$. If we were to use the Second Derivative Test to find this local minimum, why are we unable to detect the local minimum?
  9. Find all local extrema of \[f(x) = x^2 - 2x\] using the Second Derivative Test.
  10. Given this function $f(x)$ find the following:
    1. $\displaystyle\lim_{x\rightarrow 0}f(x)$
    2. $\displaystyle\lim_{x\rightarrow 2^-}f(x)$
    3. $\displaystyle\lim_{x\rightarrow 2^+}f(x)$
    4. $\displaystyle\lim_{x\rightarrow \infty}f(x)$
    5. $\displaystyle\lim_{x\rightarrow -\infty}f(x)$
    6. Find all vertical and horizontal asymptotes.

    11. The rest of these problems will appear on next week's homework. Skip the rest of these for this homework.

  11. Find the limit or show it does not exist:
    1. $\displaystyle \lim_{x\rightarrow \infty} \dfrac{3x - 2}{2x + 1}$
    2. $\displaystyle \lim_{x\rightarrow -\infty} \dfrac{4x^3 + 6x^2 - 2}{2x^3 - 4x + 5}$
    3. $\displaystyle \lim_{x\rightarrow \infty} \cos(x)$
    4. $\displaystyle \lim_{x\rightarrow \infty} (\sqrt{9x^2 + x } - 3x)$
    5. $\displaystyle \lim_{x\rightarrow \infty} \dfrac{x^2}{\sqrt{x^4 + 1}}$
    6. $\displaystyle \lim_{x\rightarrow \infty} \dfrac{x}{x^2 + 1}$
    7. $\displaystyle \lim_{x\rightarrow \infty} \dfrac{\sqrt{1 + 4x^6}}{2 - x^3}$
    8. $\displaystyle \lim_{x\rightarrow \infty} (x^2 - x^4)$
  12. Sketch a graph of the function which satisfies the following:
    • $f'(2) = 0, \ f(2) = -1, \ f(0) = 0$
    • $f'(x) < 0$ when $0 < x < 2$
    • $f'(x) > 0$ when $ x > 2$
    • $f''(x) < 0$ when $0 < x < 1$ or $x > 4$
    • $f''(x) > 0$ when $1 < x < 4$
    • $\displaystyle \lim_{x\rightarrow \infty} f(x) = 1$