4.4: Indefinite Integrals and the Net Change Theorem

Motivation

The final example in Section 4.3 involved finding the integral \[\int^2_{-1}\dfrac{1}{x^2} \ dx\]

Even though we can't use FTC Part 2 to calculate the integral, the antiderivative \[F(x) = -\dfrac{1}{x} + C\] is still valid on the domain $(-\infty, 0) \cup (0, \infty)$.

Thus you may manipulate the antiderivatives symbolically. Sometimes this is called "symbolic integration," or in modern times, we usually call it the indefinite integral.

The Indefinite Integral

The indefinite integral is equivalent to the most general antiderivative: \[\int f(x) \ dx = F(x) + C \qquad \text{means} \qquad \dfrac{d}{dx} [F(x) + C] = f(x)\]
$\displaystyle \int x^2 \ dx = \dfrac{x^3}{3} + C$

Here are a few indefinite integrals to be familiar with. They are the opposite of the derivative rules you know about! \begin{align} &\int x^n \ dx &&= \dfrac{x^{n+1}}{n+1} + C \qquad (n \neq -1) \\ &\int \sec^2 x \ dx &&= \tan x + C \\ &\int \csc^2 x \ dx &&= - \cot x + C \\ &\int \sec x \tan x \ dx &&= \sec x + C \\ &\int \csc x \cot x \ dx &&= - \csc x + C \end{align}

Find the following integral: \[\int (10x^4 - 2\sec^2 x) \ dx\]
Integrate the following: \[\int \dfrac{\cos \theta}{\sin^2 \theta} \ d\theta\]
Integrate the following: \[\int^9_1 \dfrac{2t^2 + t^2 \sqrt{t} - 1}{t^2} \ dt\]

Net Change Theorem

Integrating a rate of change gives you what's called the net change:

The integral of a rate of change is the net change: \[\int^b_a F'(x) \ dx = F(b) - F(a)\]

Let's consider the distance problem in Section 4.1.

Suppose $v(t)$ is an instantaneous velocity function for a particle moving in a straight line. Then by convention $s(t)$ is the position function.

If $v(t) > 0$, the particle moves to the right, and if $v(t) < 0$, the particle moves to the left. Here's an example $v(t)$ on a time interval $[t_1, t_2]$:

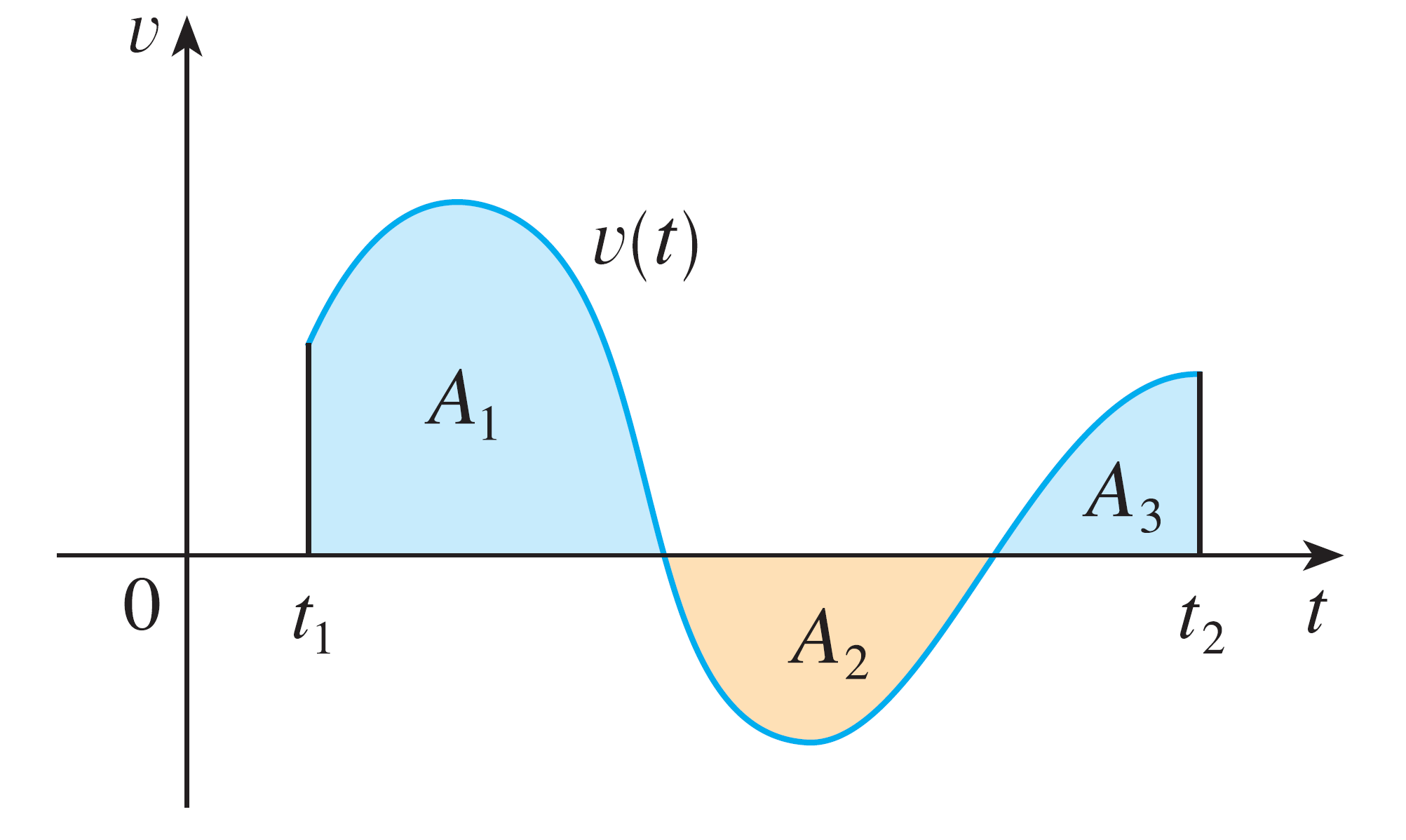
The displacement of the particle is defined as the difference between the final position and the initial position.

The distance of the particle is defined as the total unit length travelled, regardless if the particle moves left or right.

The displacement the a time interval $[t_1, t_2]$ is just the difference between the final position and the initial position, or the net change: \[\text{displacement} = \int^{t_2}_{t_1} v(t) \ dt = A_1 - A_2 + A_3\]

But the distance travelled on $[t_1, t_2]$ is different. Both $v(t) > 0$ and $v(t) < 0$ account for total distance travelled. So the formula requires you to integrate $\lvert v(t) \rvert$: \[\text{distance} = \int^{t_2}_{t_1} \lvert v(t) \rvert \ dt = A_1 + A_2 + A_3\]

Now we have the conceptual idea, let's look at the details.

A particle moves along a horizontal line so that its velocity at time $t$ is $v(t) = t^2 - t - 6$.
  1. Find the displacement of the particle on $[1, 4]$. Did the particle end up to the left or the right of the starting position?
  2. Find the distance of the particle on $[1, 4]$.